 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2011 Revised 2018
Natural Born Mathematicians
For centuries, thinkers have pondered the origins of mathematical thinking. How come humans can do maths at all? And what is maths? Is it discovered, or invented? And more prosaically, how should it be taught?

In recent years, the science of neuropsychology has brought researchers nearer to the heart of these questions, and given us some surprising insights into the way our brains work. Brain scans and carefully planned experiments on very young children - even newborn babies - have put it beyond all doubt that the fundamentals of mathematical thinking are innate to human beings. Watching the gaze of tiny babies can reveal a great deal. A baby looking away is showing signs of familiarity or boredom, whereas one staring intently is indicating surprise or interest. Researchers can use these observations to tell what expectations babies have in different situations and when those expectations aren't met.
"We are born with a core sense of cardinal number," says neuropsychologist Brian Butterworth. "We understand that sets have a cardinality, that is, that collections have a number associated with them and it doesn't really matter what the members of that set are." Cardinality is the quantity of the set and is based on mapping. In the diagram below, one circle is taken at random and given the number 1. Another is then selected and given the number 2 which is next in the sequence. One more is taken and assigned the next number, 3 and so on.
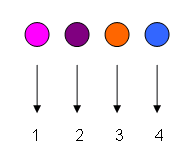
Butterworth goes on to explain: "Infants, even in the first week of life, notice when the number of things that they're looking at changes. If you show babies two things and then another two things - you can change what the things are and vary lots of the visual features of these two things, so it's not that you're showing them the same thing over and over again - they gradually lose interest and start to look away for longer and longer periods."
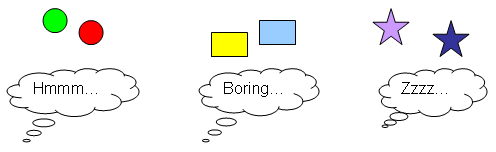
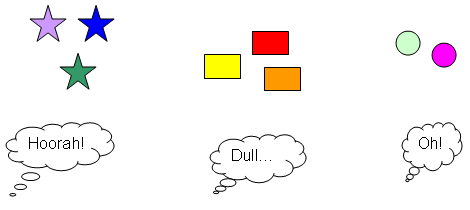
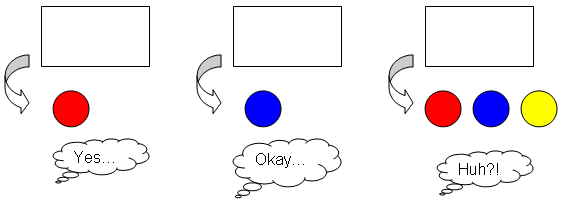
So even before babies can focus their eyes, they will be surprised to see a sum with the wrong answer! These core abilities, which Butterworth calls the "number module", may be the foundation of everything we learn about mathematics later in our lives.
The fact that we are born with some mathematical ability has some fascinating implications for our understanding of human thinking and therefore for our teaching. These studies also imply that mathematical ability can be separated from language, contrary to the findings of many eminent academics. The American Chomsky (1928-), who has a great reputation in linguistic research, believes that mathematical ability is a part of language. Piaget (1896-1980), renowned for his research in development psychology, claimed that mathematical ability doesn't start to appear at all in children until they have some elements of logical reasoning.

Butterworth, however, is suggesting that mathematical aptitude pre-empts any knowledge of linguistics. Newborn babies, commonly thought to be incapable of anything but eating, sleeping and crying, are actually budding mathematicians. We arrive in this world hardwired with basic number abilities, and very probably everything we learn later in life about mathematics builds on this fundamental
core.