 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2011 Revised 2017
Logic
What exactly do we mean by logic? The Oxford Compact English Dictionary gives the definition as:
But what does logic mean to us and is that different to mathematical logic ? We will explore these questions here.
One way to think of logic is as the understanding of how ideas are used in arguments. We often think of arguments as loud discussions between two or more people who don't agree with each other. I am sure that you can think of times when you have argued recently - perhaps it was with a brother or sister over what to watch on TV or when they should go to bed.


However, an argument can simply be putting forward ideas which explain your point of view, not necessarily in front of someone who isn't of the same opinion. If these ideas are not logical, then your argument will fall flat on its face. Let us look at this in more detail:
We use reasoning in the world around us without really thinking anything of it. For example, if I were told that David Beckham is an Englishman and that all the English are Europeans, then I can work out that David Beckham is a European. The steps that I have taken to come to this final statement involve logic. On the other hand, if I were told that Emma is in class 4G and some pupils in 4G are right-handed, then if I conclude that Emma is right-handed, I wouldn't be thinking very logically.
However, Emma could be right-handed couldn't she? It is very important to realise that logic and truth are not the same thing. It may be that Emma is indeed right-handed and I am correct, but I have not used logic to arrive at this conclusion. Similarly, David Beckham is only European if the two facts that I was originally told are true. So, even though I have used logical thinking, if in fact David Beckham isn't an Englishman then he is not necessarily European.
In coming to the conclusion that David Beckham is a European (let's assume that we know for certain he is English so our conclusion is right), we are really using our understanding of "sets" and "subsets" of these. English people are a subset of the set of Europeans. In maths, Venn diagrams are often used to show this sort of information. Below is an example which shows how you would place the numbers 1 to 15 in the sets of "Odd numbers" and "Prime numbers":
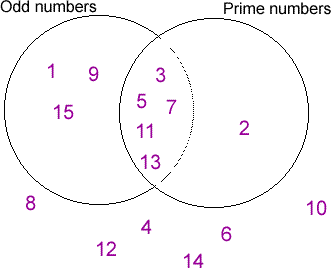
Venn diagrams frequently help us to make our deductions more quickly.
The Ancient Greeks were the first to really develop logic, in particular Aristotle who lived from 384 to 322 BC. Aristotle put forward the notion of a syllogism . This is an argument in three parts, like the examples above. A syllogism consists of two premises and a conclusion . The first premise must have one thing in common with the second premise. The second premise must have one thing in common with the first premise. The conclusion must have one thing in common with both premises. Aristotle's example is:
| i. | Every Greek is a person | -- | first premise |
| ii. | Every person is mortal | -- | second premise |
| iii. | Every Greek is mortal | -- | conclusion |
Aristotle believed that logic should be investigated before any other areas of knowledge. He made a lot of progress in the understanding of logic, but all of his analysis was done in everyday language.
It wasn't until much later that Leibniz took Aristotle's ideas a stage further. Leibniz (who lived between 1646 and 1716) was taught Aristotle's theories at school, but wasn't satisfied with them. He suggested that a scientific language needed to be developed which could be more precise than using everyday words. Leibniz got a long way in creating symbolic logic which used formulae to help work through deductions.
Boole refined these formulae to produce a special form of algebra called Boolean algebra. Mathematicians can use this to write and analyse logical ideas. Others followed in his footsteps, for example Frege and Peano who were convinced that maths could be reduced to logic. More recently, Bertrand Russell and Alfred Whitehead wanted to prove this. In the process they found that this could generate paradoxes . A paradox is an expression that seems to contradict itself, like "this statement is false" or "I am telling you the truth when I say I am a liar".
Even though Russell and Whitebread encountered these problems with mathematical logic, it is used a great deal in the world today. Boolean algebra has wide applications in telephone switching and computer technology.
The St Andrew's website http://www-history.mcs.st-andrews.ac.uk/index.html has more details on all of these logicians as well as hundreds of other mathematicians.