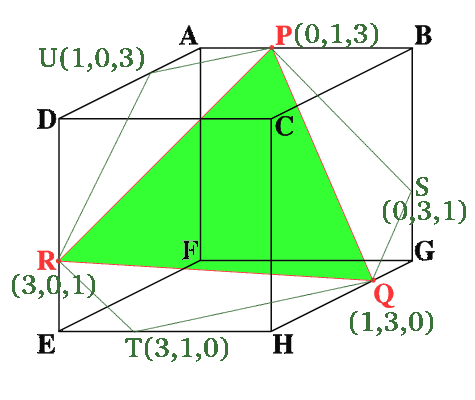
The diagram shows co-ordinate axes with origin at the point F, x axis along FE, y axis along FG and z axis along FA. The triangle PQR lies in the plane x + y + z = 4 which cuts the cube into two 'half cubes'.

The solution below is entirely the work of Alex of Woodhouse Sixth Form College.

We start with the assertion that the cube has rotational symmetry of order 3 about CF. Now, consider the transformation, T say, that rotates the cube through 120 degrees clockwise (see diagram) about CF. Thus T will map A to G, B to H, G to E, H to D, E to A and D to B.

The point P is mapped to P' say. But the line segment AB is mapped to the line segment GH. Hence the point P which is one third of the way along AB must be mapped to a point one third of the way along GH. But Q is one third of the way along GH, and so P' and Q must be coincident. It can be seen from similar lines of reasoning that T will map Q to R and R to P. Therefore the triangle also has rotational symmetry of order 3 about CF. But this can only be the case if the plane of triangle PQR and CF are perpendicular.

Now since CF and the plane of triangle PQR are perpendicular, the plane that contains triangle PQR must be symmetrical in the plane of ACHF (since the plane of ACHF contains CF). But the cube itself is also symmetrical in the plane of ACHF. Hence the cube and the plane of triangle PQR will both be mapped to themselves on reflection in the plane of ACHF. Hence the plane of triangle PQR will cut AD, EH and GB at points which are the images of P, Q and R in reflection in the plane of ACHF respectively. i.e. one third of the way along each of their lengths.

From this we can see that each 'half cube' will have rotational symmetry of order 3 about a line perpendicular to the plane of triangle PQR and passing through either C or F depending on which 'half cube' is in question. There are clearly no other symmetries for these 'half cubes'.