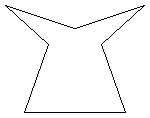
The description does not say that heptagon has to be convex, i.e. all of its interior angles need not be less than $180^{\circ}$. Since $(2 \times 7 - 4) \times 90 = 900$, the interior angles of all heptagons total $900^{\circ}$. The creation of a heptagon with all the given conditions is possible as the diagram shows. Notice that four of the interior angles are acute and the other three are reflex angles.