Copyright © University of Cambridge. All rights reserved.
'Bus Stop' printed from https://nrich.maths.org/
Show menu

There were a number of excellent solutions to this problem which revealed three basically different approaches that I think are all worth sharing. James of Audenshaw School offered the following solution and commentary, which reflects the largest proportion of your answers. I like it very much because he explains his journey very well.
Derek adopted an approach based on a graphical solution and using similar triangles. I have included his graph, for interest, below. I used a graphical approach to solve this problem the first time I met it - and I felt that my solution was quite a neat one.
The last solution, and easily the most elegant, was presented by Ian and Charlie of the William Lovell School. I have added a little to their solution for clarity but it is simple and uses no algebra - quite a surprise and very, very nice as it makes excellent use of proportionality.
What a lovely problem.We can establish from this a couple of inequalities and I was tempted to try this but decided it would be a pointless waste of time though linear programming can be fun.
A bus leaving $x$ must travel to $x+y$ and back to 145 and the bus leaving $x+y$ must travel to $x$ and then to 145. Therefore the distances for the respective buses are: \begin{eqnarray} Bus 1: x \rightarrow x+y \rightarrow 145\\ 2y - (145 - x)\\ Bus 2: x+y \rightarrow x \rightarrow 145\\ y +(145- x) \end{eqnarray} At this point it is not known which of these journeys is the longer journey. One may expect this to be important as it is the longer journey that has been under taken by the faster bus. However I can assure you that this is actually irrelevant but I will assume Bus 2 to be the faster bus. This gives the following equation:
\begin{eqnarray} \frac{y+ (145-x)}{5} &=& \frac{2y-(145-x)}{4} \\ 4(y+145-x) &= & 5(2y-145+x)\\ 1305 &=& 9x + 6y\\ 435 &=& 3x + 2y \end{eqnarray} This equation on its own is of course unsolvable, however if the same technique is applied to the 3rd meeting time an equation in terms of $x$ and $y$ will be achieved again. However although it is not relevant which bus was chosen as the faster it is very important that you select the same bus both times.
\begin{eqnarray} Bus 1: x \rightarrow x+y \rightarrow 145 \rightarrow x \rightarrow 201 \\ 2y (201 - x)\\ Bus 2: x+y \rightarrow x \rightarrow 145 \rightarrow x+y \rightarrow 201\\ 3y - (201 - x) \end{eqnarray} Again we will assume that Bus 2 is the faster bus. This will give the following equation
\begin{eqnarray} \frac{3y -(201-x)}{5} &=& \frac{2y+(201-x)}{4} \\ 4(3y-201 +x) &= & 5(2y+201-x)\\ 1809 &=& 9x + 2y \end{eqnarray} We now have two linear equations in terms of $x$ and $y$ which we need to solve: \begin{equation} 9x+2y= 1809 \end{equation} and \begin{equation} 3x+2y = 435 \end{equation} Solving these two equations we get $$x=229$$ $$y=-126$$
The negative sign for $y$ has happened because James assumed the second bus was the fastest when it was actually the first bus.
Here is the diagram Derek used for his solution. Although his final answer was wrong, the use of similar triangles can result in a reasonably elegant solution.
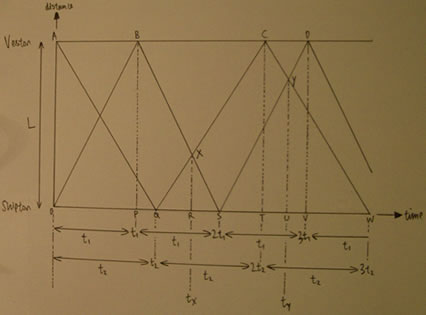
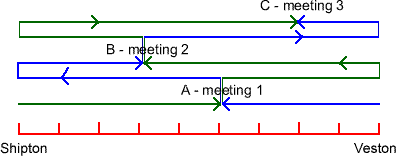
So first, divide the distance between the two towns into nine equal parts.
The first meeting place is A, the second meeting place is B, and the third meeting place is C.
The distance between B and C is : $201 - 145 = 56$
$56$ is four units and so each unit is $14$ miles.
So, to find the milestone of Veston: $201 + 28 = 229$
Milestone of Shipton: $145 - 42 = 103$