 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Timber!



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everybody who had a go at this activity. We had a few solutions suggesting that the caretaker should just go to the top of the tree and measure the height that way, but we're really looking for solutions that suggest how we could estimate the height of the tree without measuring it.
Phoenix from Good Shepherd in Australia said:
I think Mo's solution would work best because when you measure the length of the shadow of the tree, you get the same result as you would if you measured the height of the actual tree.
Good idea, Phoenix. Does it depend on how high the sun is in the sky? Could you use the cane to help you check if the length of a shadow is the same as the length of the object?
Nico also thought about how the caretaker could use the shadow of the tree to work out the height. They said:
Wait for a day in which the sun is at a 45 degree angle and then how long the shadow is will be how large the tree is. I think that to get the shadow at a 45 degree angle you need to take the time exactly between 12:00 and what time the sun sets and place a dot exactly in the middle, where that dot is is when the shadow will be at 45 degrees!
Well explained, Nico! The problem with your idea for how to get a 45 degree angle is that the sun isn't always directly overhead at 12 midday - if it was then this would be a good way of estimating the angle. Could you use either Mo or Sam's method to help you get the shadow at a 45 degree angle?
Tianchen from Pierrepont Gamston Primary School sent in this explanation:
See the picture below. The sun creates shadows of a cane and a tree so we have two similar triangles. If we measure the shadows of the cane and the tree at the same time, the ratio of corresponding sides from the similar triangles is equal.
So, AE: AC= DE: BC, or 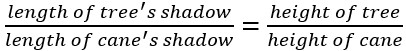 .
.
What do I know?
I know that the height of the cane (BC) is 1m. The length of the cane’s shadow (AC) can be measured. For example, we assume it could be 2m. Suppose the length of tree’s shadow (AE) is 100m.
How do I work out the height of the tree (DE)?
Substitute the known values into the equation above.
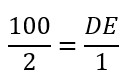
We need to divide 2 by 2 to get one then to keep the equivalent fractions divide 100 by 2 which is 50. DE=50m.
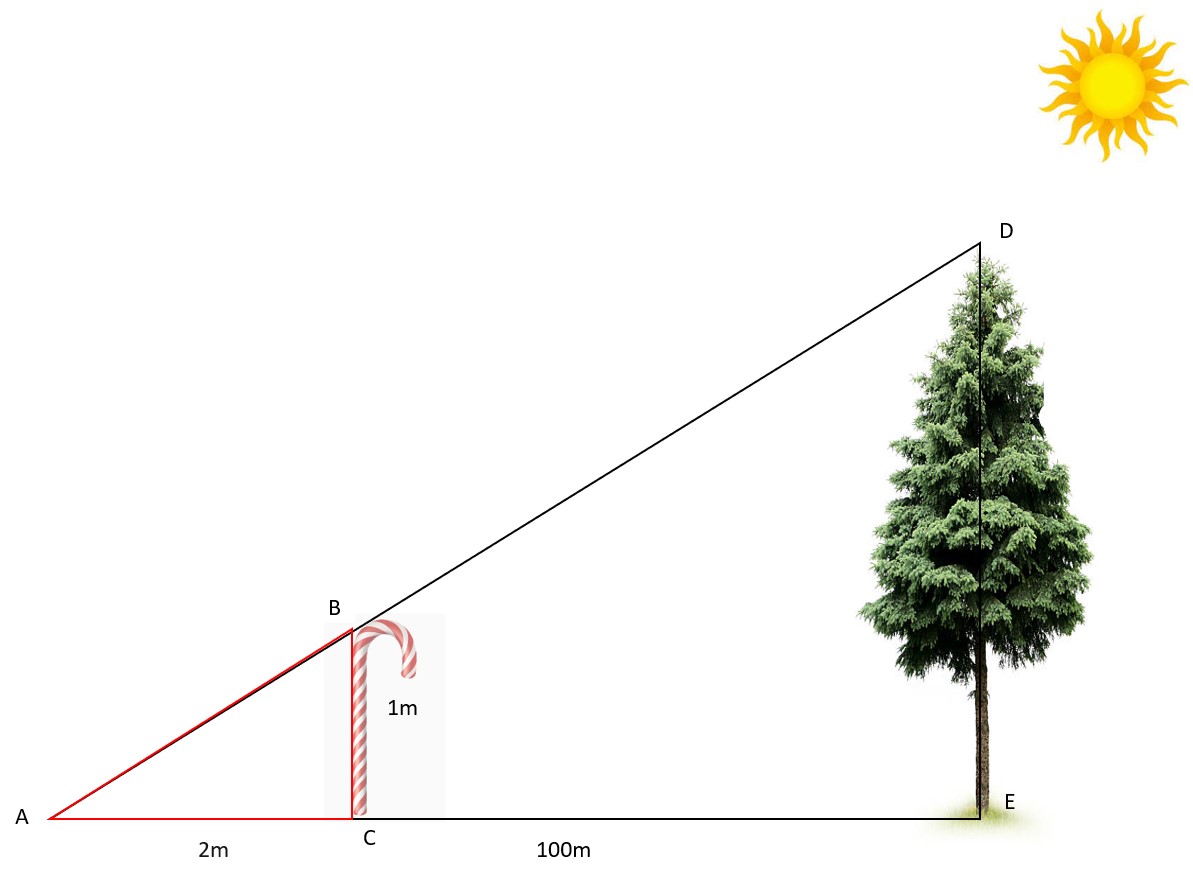
Well done for explaining that so carefully, Tianchen. In this picture, Tianchen has positioned the cane so that the end of the cane's shadow reaches the same point (A) as the end of the tree's shadow, but this method would still work even if we made two different triangles with the cane and the tree.