 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Robot Monsters



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had a couple of very full solutions to this problem. Jack and Alex from Woodfall Junior School wrote:
The biggest robot you can make is 22cm using 6cm head 8cm body and 8cm legs
The smallest robot you can make is 14cm using 3cm head 5cm body and 6cm legs
The bits that are left over using 4cm head 7cm body and 7cm legs that equals 18cm
They went on to say:
|
Head |
Body |
Legs |
Total height |
|
3 |
5 |
6 |
14 |
|
3 |
5
|
7
|
15 |
|
3 |
5
|
8
|
16 |
|
3 |
7
|
6
|
16 |
|
3 |
7
|
7
|
17 |
|
3 |
7 |
8
|
18 |
|
3 |
8
|
6
|
17 |
|
3 |
8 |
7 |
18 |
|
3 |
8 |
8 |
19 |
|
6 |
5 |
6 |
17 |
|
6 |
5
|
7
|
18 |
|
6 |
5
|
8
|
19
|
|
6 |
7
|
6
|
19 |
|
6 |
7
|
7
|
20
|
|
6 |
7 |
8
|
21 |
|
6 |
8
|
6
|
20 |
|
6 |
8 |
7 |
21 |
|
6 |
8 |
8 |
22 |
|
4 |
8
|
8
|
20 |
|
4 |
8
|
7
|
19 |
|
4 |
8 |
6 |
18 |
|
4 |
7
|
8
|
19 |
|
4 |
7
|
6
|
17 |
|
4 |
7 |
7 |
18 |
|
4 |
5
|
8 |
17 |
|
4 |
5
|
7 |
16 |
|
4 |
5
|
6
|
15
|
We tried to use a systematic order to make sure we found all 27 monsters. We found all the monsters with 3cm heads first, then 6cm, then 4cm. We did the same with the bodies and legs.
Ruth from Swanborne House School commented:
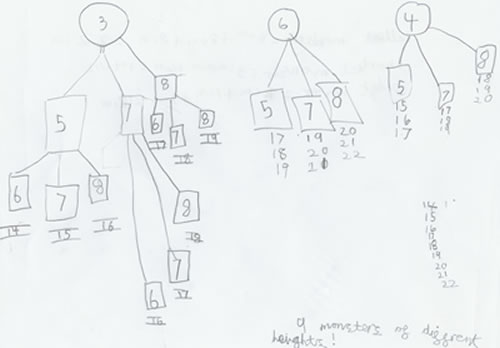
There are 9 possible monster heights between 14cm and 22cm (14/15/16/17/18/19/20/21/22). To prove that you could make all of them we drew a diagram of all the possible combinations, starting from the three heads. We found that once we had drawn the first head + body and leg combination for the 3cm head, we could work out the other combinations for the 3cm head quite easily, because only the body measurement varied. Then we found it was easy to adjust from this to the other two heads, and we didn't need to do the full diagram.
Here is the diagram that Ruth sent:
Children from Seven Mills Primary School in the London borough of Tower Hamlets created robots with the body part cards but then used Numicon pieces to represent the height of each part. This meant that they were easily able to compare the heights of their robots and spot which ones were missing. Here are some photos to show what they did:


Three very good ways of solving this problem - well done!