 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
You Never Get a Six



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
You Never Get a Six
It was raining and Tom, Vincent, Charlie and Edward had been playing a game with dice during break.
"You never get a six when you want one," grumbled Charlie, "I'm sure sixes come less than the other numbers!"

Miss Brown heard him.
"You can all try throwing dice and noting what you get," she said, "It fits in quite well with the work we are going to do next. Throw the dice and make a list of what you get. See if you get less sixes then."
"It's only when it matters if you get a six," grumbled Charlie.
Miss Brown thought for a moment.
"I'll give a Team Point to the one who gets the most sixes," she said, "Mind you, no cheating!"
"Wow!" exclaimed Vincent.
The boys worked in pairs and made lists of their throws. They all threw the dice the same number of times. Here is the list that Tom made for Edward's throws:

They decided to make each of the numbers on the dice a different colour when they recorded the work so they could compare them easily.
Here is the graph Edward made from his figures:
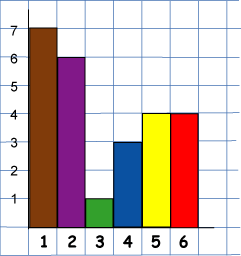
Here is Charlie's unfinished graph (he hasn't labelled anything yet):

Here is Tom's unfinished graph:

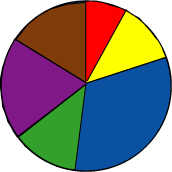
Here is Vincent's unfinished pie-chart:
Who won the Team Point for the most sixes?
How many $1$s, $2$s, $3$s, $4$s, $5$s and $6$s were thrown altogether?
What percentage (or: How many out of $100$) of the throws were sixes?
Why do this problem?
Possible approach
Key questions
Possible extension
Learners could make graphical representations of their own dice throws or do How Big Are Classes 5, 6 and 7?Possible support
Suggest trying The Pet Graph first which is simpler and easier to understand.You may also like
Roll These Dice
Roll two red dice and a green dice. Add the two numbers on the red dice and take away the number on the green. What are all the different possible answers?
Stop or Dare
All you need for this game is a pack of cards. While you play the game, think about strategies that will increase your chances of winning.
Game of PIG - Sixes
Can you beat Piggy in this simple dice game? Can you figure out Piggy's strategy, and is there a better one?