Copyright © University of Cambridge. All rights reserved.
Ruth from Swanborne House School sent in a well-explained solution and I have added some diagrams to it:
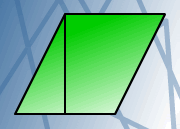
When you take away the right-angled triangle, you are left with an irregular quadrilateral. This has one short side which is the same size as the short side of the triangle. If you put these two edges together you get a large triangle:

There are two remaining sides on the quadrilateral which are both the same size. If you match the triangle up with these sides (using the side which forms the right angle with the shorter side), you get either a parallelogram or another irregular quadrilateral:
You can't use the fourth side of the irreguar quadrilateral again, because you get back to a square again. So we think you can only make three shapes, unless you are allowed to flip the pieces.
Thank you for a well thought out solution, Ruth.
A, from Zion Heights Junior High School, did look at what happens when you flip the pieces over. Here is what he or she said:
The square has been cut into a trapezoid (or trapezium) and a right-angled triangle and since only matching sides can be connected to form a new shape, we should start by identifying pairs of sides - one from each smaller shape - that are of the same length.
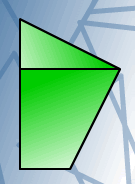
The hypotenuse (longest side) of the right-angle triangle is the same length as the edge of the trapezoid from which it had been detached. If you flip the triangle along a diagonal line of reflection (sloping down from left to right) and refit it to the trapezoid, a pentagon is formed:
The shorter leg of the triangle matches the shortest side of the trapezoid. From this pairing, the outcome is two possible new shapes: the triangle can be rotated $180^\circ$ and lined up to form a big right-angled triangle (like Ruth's first shape above); or the mirror reflection (along a vertical line of reflection) of its rotated $180^\circ$ form can be
matched up to form a sort of pentagon:
The longer leg of the triangle matches the uncut sides of the original square - the two second longest sides of the trapezoid (or trapezium). On the left edge, two shapes can be formed: a parallelogram by a simple translation of the small triangle (Ruth's second shape above); or a larger trapezoid with the mirror reflection (along
a horizontal line of reflection) of the translated triangle:
On the top edge, two more shapes can be formed with a rotated version of the original triangle (Ruth's third shape) and the reflection (along a vertical line of reflection) of the rotated version:
So, we've got seven new shapes altogether.
Heather from Cottenham Primary school sent us a picture of the shapes she made. She explained that her mummy helped with the names:

Well done to you all and thank you for sending us your work.