We received many good solutions for this challenge. 

Mikey from Archbishop of York CE Junior School wrote:

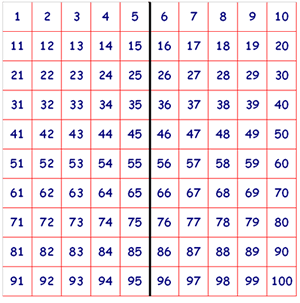
Having printed the page out I realised that if you turned it over you could see through the page. Looking where $100, 58, 23, 19$ would be meant you could read off the answers as $91, 53, 28, 12$. Or is this cheating?

I don't think this is cheating at all Mikey! Mikey then realised something else which was also spotted by "N" (he or she didn't give us a full Christian name):

If you draw a mirror line down the middle of the square you will be able to work out what number will be behind each number. You choose a number, then find its mirror on the other side of the line, this 'mirror' number will be the number on the reverse!

This is also a very handy method - well noticed. "N" sent an image with the "mirror line" drawn in:

Devonshire Maths Club, Devonshire Primary School have found a pattern which they describe:

St Non's Class at St Mary's in Wales wrote:

We found this problem interesting and challenging.
Behind 100 would be 91. Behind 58 would be 52. Behind 23 is 28 and lastly behind 19 would be 12.

We counted how many space from the left it was, if it was 4 from the left it would also be 4 spaces in from the right.
We also knew that 5 was in middle and it would be matched with a 5 on the other side.

We tried adding the numbers on opposite sides together. We noticed that 1+10 = 11, 11+20 = 31, 21+30 = 51 and so on. These numbers went up in 20s.

We then tried the next line in 2+9 = 11, 12+19 = 31, 22+29 = 51.
These numbers also went up in 20s. We thought this was interesting.

We went to try the third row in 3+8 =11.... it was the same!!!
These are the patterns we noticed.

Thank you for information about the patterns that you found. I wonder whether you can explain why these patterns appear?