Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Bend
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
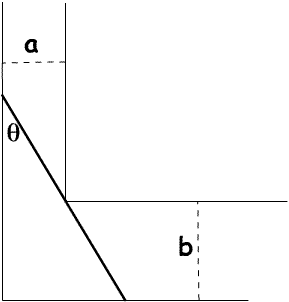
This solution comes from Andrei Lazanu ,Tudor Vianu National College, Bucharest, Romania.
I calculate the length of the stick in terms of $a$, $b$ and $\theta$. From the figure I observe that the length of the stick could be seen as the sum of two hypotenuses of two right-angled triangles. Its length is: $$l(\theta)= {a\over \sin \theta} + {b\over \cos \theta}.$$ Now, I have to calculate the minimum of this expression, in order to make the stick pass through the corner. For this, I calculate the derivative of $l(\theta)$ and equate it to $0$. I must say from the beginning that derivatives are not so familiar to me. For a minimum value of the length: $${\rm{d}l\over \rm{d}\theta} = {-a\cos \theta \over \sin^2 \theta} + {b\sin \theta \over \cos^2 \theta}=0.$$ So for a minimum value $a\cos^3 \theta = b\sin^3 \theta$ and $$\tan \theta = \left({a\over b}\right)^{1/3}.$$ Now, I have to calculate $\sin\theta$ and $\cos\theta$ as functions of $\tan\theta$. I know that: $$\cos x = {1\over \sqrt{1+\tan^2x}}$$ and$$\sin x = {\tan x \over \sqrt{1+\tan^2x}}$$ In the case of the problem, I have: $${1\over \cos \theta }= \sqrt{1+\left({a\over b}\right)^{2/3}}$$ and $${1\over \sin \theta } = \left({b\over a}\right)^{1/3}\sqrt{1+\left({a\over b}\right)^{2/3}}$$ So the minimum length is $$\eqalign{ {a\over \sin \theta} + {b\over \cos \theta} &=\left(a^{2/3}b^{1/3} + b\right)\sqrt{{a^{2/3}+b^{2/3}\over b^{2/3}}} \cr &= \left(a^{2/3} + b^{2/3}\right)^{3/2}}.$$ The result is symmetric in $a$ and $b$.
If $a=65 \text{ cm}$ and $b=75 \text{ cm}$ then $65^{2/3}+ 75^{2/3}=16.16623563 + 17.78446652=33.95070215$ and $33.951^{3/2}=197.8213407$ so an object of about $197 \text{ cm}$ could be manoeuvred around the bend but it is not possible to manoeuvre a $200 \text {cm}$ object around this bend.
You may also like
Generally Geometric
Generalise the sum of a GP by using derivatives to make the coefficients into powers of the natural numbers.
Exponential Trend
Find all the turning points of y=x^{1/x} for x>0 and decide whether each is a maximum or minimum. Give a sketch of the graph.
Slide
This function involves absolute values. To find the slope on the slide use different equations to define the function in different parts of its domain.