Thousand Words

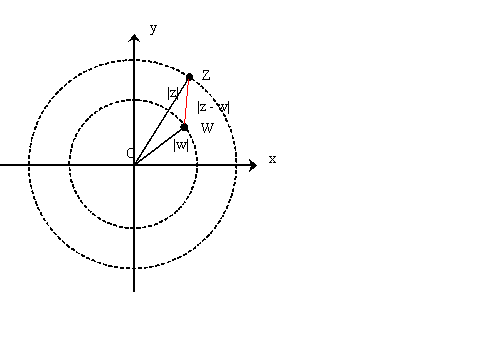
In this representation, working with complex numbers is similar to working with vectors. The two complex numbers can be added and subtracted as vectors. So, to subtract them, it is the same as adding one to the opposite of the other. The result is represented in the figure. The distance between the two points representing the complex numbers $z$ and $w$ is the modulus of $z-w$ written as $|z-w|$. The lengths of the sides of the triangle in the diagram are $|z|$, $|w|$ and $|z-w|$.

The shortest distance between any two points where one is on each circle is given by the difference of the radii of the two circles $|z|-|w|$. This would be the distance between the points $z$ and $w$ if they had the same argument. If $z$ and $w$ have different arguments then the distance between the points will be $|z- w|$ and hence $|z-w|\geq |z| - |w|$.

For the second part, mark points $A$ and $B$ on the unit circle to represent $e^{i\alpha*}$ and $e^{i\beta*}$ respectively where $\alpha*$ and $\beta*$ lie between 0 and $2\pi$. To include all possible values of $\alpha$ and $\beta$ we have $\alpha =\alpha* +2m\pi$ and $\beta = \beta* + 2n\pi$ for some integers $m$ and $n$. Clearly $A$ and $B$ also represent $e^{i\alpha}$ and $e^{i\beta}.$

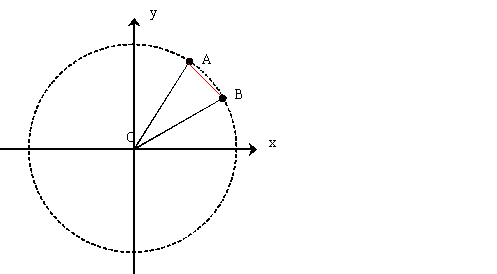
The chord length $AB$ is less than or equal to the arc length $AB$. Hence $$|e^{i\alpha}-e^{i\beta}|\leq \alpha - \beta.$$