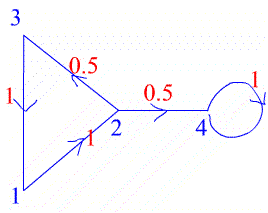
The numbers on the edges of this graph give the probabilities of a particle travelling along those edges in the direction given by the arrow. The same information is given by the entry $a_{ij}$ in the following matrix which gives the probability of travelling from vertex $i$ to vertex $j$. $$A=\left( \begin{array}{cccc} 0 &1 &0 &0 \\ 0 &0 &0.5 &0.5 \\ 1 &0 &0 &0 \\ 0 &0 &0 &1 \end{array} \right)$$

For this question you can use a graphic calculator or computer software to find powers of the matrices but you need to understand the definition of matrix multiplication (see the Thesaurus) to be able to do the question.

Can you see why the square of the matrix gives the probabilities of travelling from one vertex to another in two stages and the $n$th power of the matrix gives the probability of traveling from one vertex to another in $n$ stages? For example $$ A^{20}=\left( \begin{array}{cccc} 0 &0 &0.008 &0.992 \\ 0.008 &0 &0 &0.992 \\ 0 &0016 &0 &0.984 \\ 0 &0 &0 &1 \end{array} \right) $$ This matrix shows that there is zero probability of getting from vertex $1$ to vertex $2$ in $20$ stages (that is along $20$ edges with the paths along the edges being repeated), but there is a probability of $0.008$ (to 3 significant figures) of travelling from vertex $1$ to vertex $3$ in $20$ stages.

Work out $A^{21}$ and $A^{22}$ and explain the occurrences of zero and non zero entries in these matrices.

What would you expect to happen for higher powers, (e.g. $A^{100}$), and why?