Copyright © University of Cambridge. All rights reserved.
'Maximum Flow' printed from https://nrich.maths.org/
Show menu
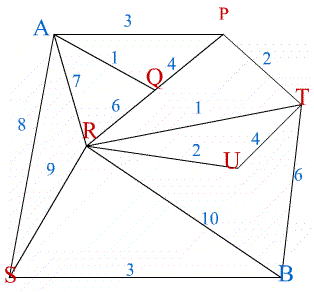
The graph represents a supply network from $A$ to $B$ and the numbers on the edges of the graph show the maximum capacity for flow in each of the sections.
Imagine any straight line cutting through edges of the graph (but not through vertices) such that $A$ is on one side of the line and $B$ is on the other. All the flow from $A$ to $B$ has to go along the edges cut by your line so the total flow from $A$ to $B$ is less than or equal to the sum of the flows along those edges. Considering all possible such cuts, why is it that the maximum flow
from $A$ to $B$ is less than the minimum sum for all cuts? Find the maximum flow in this example.
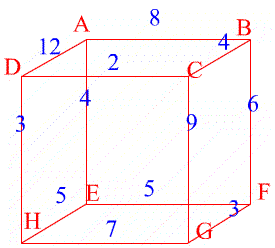
In the second example the network is a cube. Find the maximum flow from $A$ to $G$.