Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cube Net
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Congratulations Andrei, School No. 205, Bucharest, Romania on another excellent solution.
1. I observed that a cube could be represented by the diagram below, that keeps all edges and vertices (the lengths are not important).
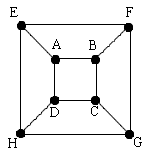
From the beginning I observe that one could start from any vertex in a cube and there are $8$ vertices.
From any vertex there are three possible routes. I shall consider the routes starting from vertex $A$.
Below are written all the possible combinations I found starting with the edge $AD$:
| Path | Circuit |
| A-D-C-B-F-E-H-G | No |
| A-D-C-B-F-G-H-E-A | Yes |
| A-D-C-G-H-E-F-B-A | Yes |
| A-D-C-G-F - impossible | |
| A-D-H-E-F-B-C-G | No |
| A-D-H-E-F-G-C-B-A | Yes |
| A-D-H-G-C-B-F-E-A | Yes |
| A-D-H-G-F-E - impossible |
I observe that there are $6$ possible paths, $4$ of which are Hamiltonian Circuits.
I have to multiply the number of solutions I obtained. So the total number of solutions is given by $8 \times3 \times6$ that is $144$, and $96$ are Hamiltonian Circuits.
Because all vertices of the cube are indistinguishable, there are $18$ solutions, and $12$ Hamiltonian Circuits.
2. Set $\{a, b, c\}$ has the following subsets: $\{a, b, c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a\}, \{b\}, \{c\}, \phi $. I observe that they could be arranged so that one subset is connected with $3$ other subsets that differ from the first by only one element, deleted or inserted. These subsets can be positioned on the vertices of a cube.
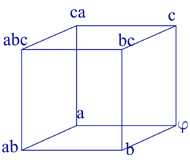
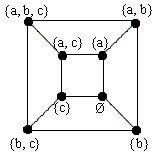
I have verified that each subset is connected with $3$ other
subsets, forming a diagram as found before, or, more intuitively, a
cube. So, the problem is reduced to the first problem.
The number of sequences is $144$ sequences, or $18$ if the
first element of the sequence does not matter.