Copyright © University of Cambridge. All rights reserved.
'All Tied Up' printed from https://nrich.maths.org/
Show menu
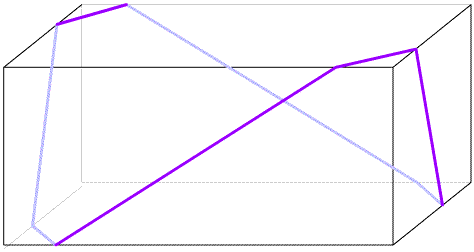
I like to run a ribbon around the box so that it makes a complete loop with two parallel pieces of ribbon on the top (and on the bottom) of the box.
The ribbon crosses every face once, except the top and bottom, which it crosses twice.
The ribbon rests tightly against the box all the way round because the angle at which it meets a corner is continued onto the next face.
I can cut the ribbon in advance of placing it around the box and I can slide the ribbon around a little to position it.
If the box is $20 \text{ cm}$ by $10 \text{ cm}$ by $5 \text{cm}$ - how long will the ribbon be?
Show why it is possible for me to "slide" the ribbon.
What will it be for any box with height $h$, width $w$ and length $l$? (n.b. the length and width are the longer distances and form the top of the box. Would the string be longer or shorter if this was not the case?)