Lost in Space

Derek (no school given) offered the following insights into this problem: - and nicely explained too - thank you Derek.

From observation, we compile the table below:

n-row pyramid	Ways to count 1-2-3-...
1	1
2	3
3	7
4	15
...	...

The pattern can be deduced by considering route backwards, i.e. from n back to 1. The general n-row pyramid is shown below:


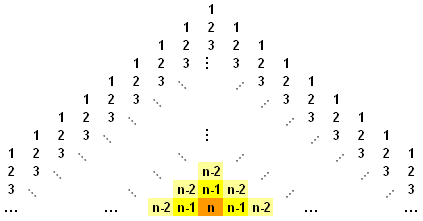
Starting at the orange square, we assert that there are 0 routes leading to the final square:

1 step earlier, at the bright yellow squares, there is 1 route leading to the final square:

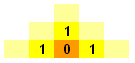
1 step earlier, at the light yellow squares, the situation becomes slightly different.The top, left and right squares all have 1 route leading to the final square. However, the middle squares have 2 routes as they each connect to 2 bright yellow squares (each of which are routes leading to the final square):


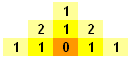
1 step earlier, the top, left and right squares all have 1 route whilst the middle squares have 3 routes as they each connect to 2 light yellow squares, bearing a total of 3 routes. We repeat this reasoning and get the following pattern:

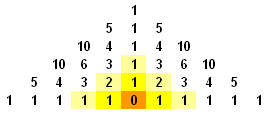
It is clear that these are the binomial coefficients. 2 of Pascal's triangles have been arranged together and the numbers along the two slanted edges represent how many ways to count 1-2-3-...-n. For example, in the diagram of the 6-row pyramid above, we see that there are 1+5+10+10+5+1+5+10+10+5+1 = 63 ways to count 1-2-3-4-5-6.

We further notice that 1, 5, 10, 10, 5, 1 are the binomial coefficients $5 \choose {k}$ $,k = 1, 2, 3, \cdots, 5 $. We generalise by claiming that the number of ways of counting $1-2-3-...-n$ is twice (because there are two Pascal's triangles) the sum of all the binomial coefficients of the $n-1^{th}$ row minus 1 (because of the overlapped 1 down the central column) which can be written as $2\sum_{k=0}^{n-1}$ ${n-1}\choose{k}$ $ - 1$.

Editor's comment: at this point it may be worth mentioniing that the sum of the binomial coefficients are powers of 2. Why?

Chen of the Chinese High School took a slightly different approach (similar to the one offered by Andrei of Tudor Vianu National College):