Copyright © University of Cambridge. All rights reserved.
'Lots of Lollies' printed from https://nrich.maths.org/
Show menu
This activity produced some good solutions.
Pooja at at the International School in the Seychelles sent this message:
To get my answer I used the two times table. When there were two kids my answer was three. Then I used the five times table when three more kids came along. I said that if each child gets one and two leftover it must mean that the answer must be seven.
Felix from Henleaze Junior wrote:Ӭ
First I worked out that there were two children and one lolly left over. So I tried 3. But then I worked out that there were then three more children which made 5 so it couldn't be 3. Then I worked out that there were two remaining when 3 more people came and I added the total number of people to the two remaining lollies and got 7. Then I went back to the two people and checked if it would
work with the two people and it did, so one possible answer is 7.
But after that I figured out that if you add 10 it would mean that there were 17 lollies and it will still work because 2 people would then have 8 each and one remaining and 5 people would have 3 each and two remaining.
Adelle and Amanie, also at the International School in the Seychelles wrote:
With two people it must be odd.
With five people, we know 7 works.
We tried adding 5 but it came to an even number. Then we added 10, it always works.
These numbers work with 2 people: 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61
These numbers work with 5 people and 2 people: 7, 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117, 127, 137, 147, 157, 167, 177, 187, 197, 207, 217

Children from Culgaith School in the UK sent in the following:
Nathan said that the answer has to be an odd number as it is shared between two children with 1 left over. We found the first solution was 7 - Emma said this. We then tried to find out if there were any other answers. We tried 8 - but then realised that this was an even number so we looked at 9 - too many left over. We looked at 11 - this time too few left over.
Alex suggested 17 - why did he choose this? He said the numbers were "basically the same". Mr Dodd said this wasn't quite true as he would rather have 17 chocolate bars than 7!
Millie said that the 10 lollipops different between 7 and 17 would give each of the two children two lollipops each and so 17 would work. We checked this out and it did! We then used the number square to show us all the solutions up to 100 - they all end in "7". We worked out that this was because the tens digit would alway share out evenly between 5 children and the 7 would give each child 1 lollipop and have two left over.
Daniel, who didn't say which school he goes to, also agreed that the numbers all end in a 7.
Poppy from Steeple Morden Primary wrote:
Thank you Poppy. I like the way you have thought about the practical side of the problem at the end and have decided how many lollies the children are likely to have had.
Deidre at Calgary Science School in Canada had a really lovely suggestion. Her Grade 4 class approached a similar problem they called The Candy Problem. They posted a video of how students arrived at the solutions. Thank you so much for that it's certainly worth watching!
Stella from Chigwell School in England wrote a very thorough account of the challenge:
Because they start off with 2 children and they share them out equally you have to divide by 2 but so that it does't go in exactly you have 1 left over which means that it has to be an odd number. But when they have just finished sharing them out properly 3 more children come along making the total of children go up to 5, so now you have to divide by 5 so it can't be any thing ending in 9, 3, 5 or 1 so that only leaves 7.
Simran from Maurice Hawk School in the USA, also had a very systematic approach. He said:
At first, I noticed that the number of lollies that I was splitting had to be be an odd number or there would not have been anything left over. So, I made this table:
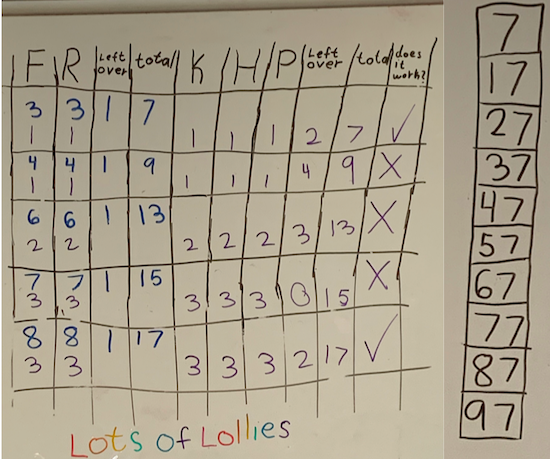
The blue shows the number of lollies that Francis and Rishi share and the purple shows the lollies that Frances, Rishi, Kishan, Hayley and Paul share. I tried a few different odd numbers and found that only a total of 7 lollies worked. Then I saw that 17 also works. Then I thought of the 100s chart and the 7s column. All the numbers in that column
would work. I checked with a big number like 87 and it worked.

And here is Phoebe's:
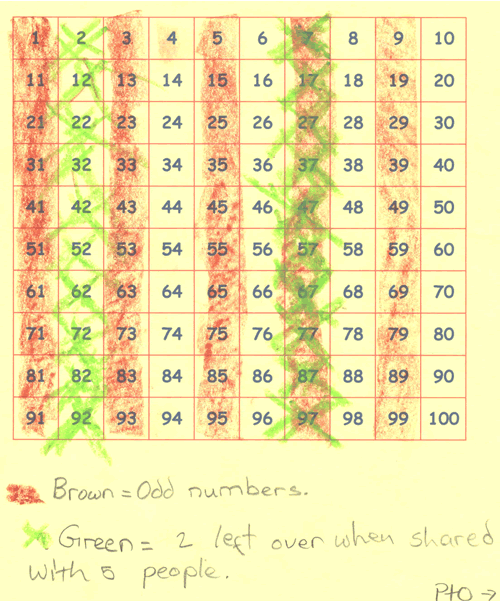
You can see that they have shaded all the odd numbers in brown and put a green cross through all the numbers that have 2 left over when shared between 5. They conclude that the number of lollies in the bag could be:
... any number that ends with a 7: 7, 17, 27, 37, 47, 57, 67, 77, 87, 97 ...
Well done both of you - you have shown how the number square is a very useful tool.
Several pupils from Warren Road Primary School sent solutions, including Ayush, Vihaan, Vishwaksen and Sarthak. This solution summarised their findings:
The two conditions:
When there are two children, 1 lollipop must be left over.
When there are five children, 2 lollipops must be left over.
At the beginning, there are two children. They share the lollies evenly. If the bag has 7 lollies, they could give themselves 3 each and there would be 1 left over. But then their their friends come along. Now there are 5 people. Still with 7 lollies, they could give themselves 1 each and have 2 leftover. This meets the requirements, so 7 is one of the answers.
After working out this solution, we realised the pattern:
When the number 5 is multiplied by any odd number and has 2 added to it, it is a solution of how many lollies are in the bag.
You have expressed this in a general way, which is very helpful. Mathematicians love to generalise!
Thank you for all these solutions which were all thought about in a slightly different way. There usually is a variety of possible ways of approaching problems.