Copyright © University of Cambridge. All rights reserved.

'Lots of Lollies' printed from https://nrich.maths.org/

Show menu

Lots of Lollies

 

If you are a teacher, click here for a version of the problem suitable for classroom use, together with supporting materials. Otherwise, read on ...

 

Frances and Rishi were given a bag of lollies.

They shared them out equally and had one left over.

Just as they had finished sharing them their friends Kishan, Hayley and Paul came along. They wanted some lollies too so the children shared them out again between all of them. This time they had two lollies left over.

How many lollies could there have been in the bag?

 

Once you've had a chance to think about it, click below to see how three different groups of pupils began working on the task.

Sarah, Danielle and Sally said:

"We noticed that $17$ works as when there are only two of them they get $8$ each, with one left over. But when their friends come along they get three each with $2$ left over.

We also notice that $7$ works and $27$ works, as well as $107$."

 

Poppy began like this:

If the two children end up with one lolly it must be an odd number of lollies. Then three more children come making the total number of children $5$. Say they had $1$ lolly each when they shared them, the number of lollies would be $7$ because $1$ times $5$ is $5$ add on $2$ for the left over ones and it makes seven. If we carry this on to $10$ lollies each it shows:


$1$ lolly each - $7$ lollies
$2$ lollies each - $12$ lollies
$3$ lollies each - $17$ lollies
$4$ lollies each - $22$ lollies
$5$ lollies each - $27$ lollies
$6$ lollies each - $32$ lollies
$7$ lollies each - $37$ lollies
$8$ lollies each - $42$ lollies
$9$ lollies each - $47$ lollies
$10$ lollies each - $52$ lollies

 

Here is the start of Phoebe and Alice's work:

 

Can you take each of these starting ideas and develop it into a solution?

Can you adapt each of these strategies to find the number of lollies when there are three friends to start with and two friends join them?
How many lollies could there be in the bag if there was 1 lolly left over to start with, and then 1, 2, 3 or 4 lollies left when they were shared between the five children?
Or 2 lollies left over to start with...?
 

What if we started with four friends, and two more friends join them...?

Why do this problem?

This problem requires children to apply their knowledge of factors and multiples, and it is a good way of making the link between sharing, division and multiples/factors. It may also be used to introduce learners to the fact that a problem can have more than one solution and that the solutions can be generalised. It can be approached in many different ways so can be a useful context in which to talk about different ways of recording and different methods of solving problems.

In conjunction with the other tasks in this group, this task also offers the chance to focus on any of the five key ingredients that characterise successful mathematicians. 

 

Possible approach

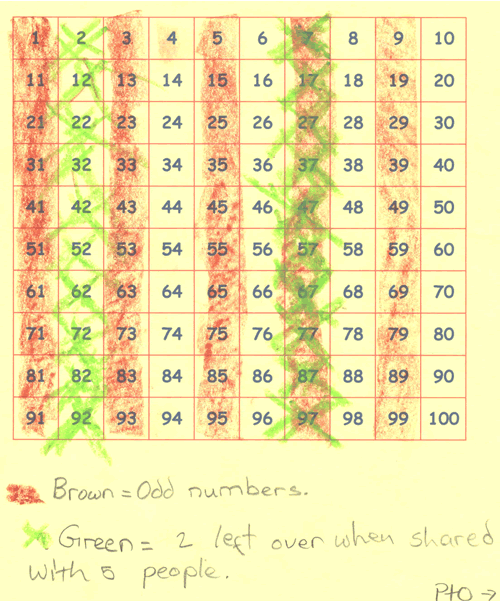
You could introduce this challenge by acting it out.  Invite two children to the front of the class and ask everyone to imagine that you have a bag of lollies.  Explain that you give them out to the two volunteers so that they have the same number each, but there is one left in the bag.  You could mime giving out some lollies so that everyone gets the idea.  Then invite three more children to the front.  Mime gathering the lollies back into the bag and then distributing them equally again, this time explaining that you have two left over.  Pose the question "I wonder how many lollies could have been in the bag?". 

Give the class a few minutes to consider, individually, how they might go about tackling the problem, then pair them up and suggest that they talk to their partner about their ideas so far.  Try to stand back and observe, and resist the temptation to make helpful suggestions!

Allow pairs to work on the task so that you feel they have made some progress, but do not worry if they have not completed it or if they report being stuck.  The aim at this stage is for everyone to 'get into' the problem and work hard on trying to solve it, but not necessarily to achieve a final solution.

At a suitable time, hand out this (doc, pdf) to pairs.  Suggest to the class that when they've finished or can't make any further progress, they should look at the sheet showing three approaches used by children working on this task.  Pose the question, "What might each do next? Can you take each of their starting ideas and develop them into a solution?".  You may like pairs to record their work on large sheets of paper, which might be more easily shared with the rest of the class in the plenary. 

Allow at least fifteen minutes for a final discussion.  Invite some pairs to explain how the three different methods might be continued.  You may find that some members of the class used completely different approaches when they worked on the task to begin with, so ask them to share their methods too.  You can then facilitate a discussion about the advantages and disadvantages of each.  Which way would they choose to use if they were presented with a similar task in the future? Why?

 

Key questions

How many children are there altogether when they share the lollies the second time?
What is the smallest number of lollies there could be?
Is this the only number of lollies there could be?
Tell me about this approach.  What do you think she/they were doing?
How do you think this will help to solve the problem?
What do you think she/they would have done next?

 

Possible extension

At the highest level, encourage learners to articulate a full generalisation about what kind of numbers of lollies there could be in the bag. This might be worded in terms of multiples, or in terms of the units digit of possible solutions.
 
Encourage learners to adapt each of the strategies to find the number of lollies when there are three friends to start with and two friends join them.
How many lollies could there be in the bag if there was 1 lolly left over to start with, and then 1, 2, 3 or 4 lollies left when they were shared between the five children?
Or 2 lollies left over to start with...?
Challenge learners to explain why some possibilities are impossible when we start with four friends, and two more friends join them.
 
The tasks in this group would be useful follow-up to this one.

 

Possible support

Learners might request a range of different resources to help them tackle this challenge, for example a hundred square, or some counters/cubes.  Try not to pre-empt their requests by placing equipment out on tables at the start, but do make sure these kind of resources are easily accessible to the children, should they want to use them and do your best to accommodate any requests which you hadn't anticipated!