Copyright © University of Cambridge. All rights reserved.
'A Chain of Eight Polyhedra' printed from https://nrich.maths.org/
Show menu
These two 3-D shapes, the tetrahedron and the octahedron have the same 2-D shape, an equilateral triangle, as their faces.
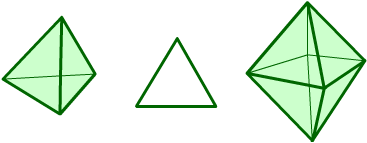
Can you arrange the shapes below in a chain so that each one shares a face (or faces) that are the same shape as the one that follows it? (The faces do not have to be the same size.)
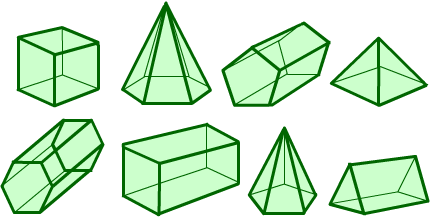
How many ways can you find to make a loop (a closed chain)
using all the shapes so that each one shares a face (or faces) that
are the same shape as the one that follows it?