Copyright © University of Cambridge. All rights reserved.
'Cut Nets' printed from https://nrich.maths.org/
Show menu
Cut Nets
The net of a cube has been cut into two. It could be put together in several ways so that it could be folded into a cube.
Here are the nets of $9$ solid shapes. Each one of these has been cut into $2$ pieces, like the net of the cube.
Can you see which pieces go together?
Why do this problem?
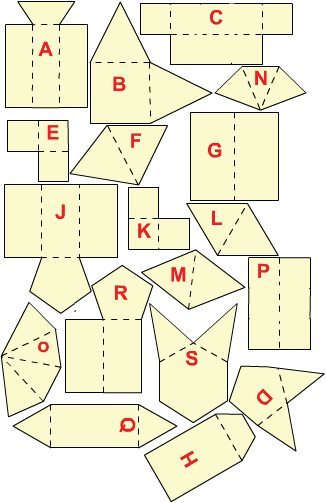
This problem makes children think hard about the nets of various polyhedra. It is not enough to know roughly what they look like. The number and shape of the faces and the way they are connected are important. It will help to develop children's visualisation skills and increase their familiarity with appropriate vocabulary. It provides an excellent opportunity for describing properties of 3D shapes.
Possible approach
You could start by talking about properties of some solid shapes with the group. One way to do this might be to hold up two shapes and ask them to talk about their similarities and differences. Depending on the children's experience you may need to explain what a net is, but they don't necessarily need to have worked extensively with nets in order to have a go at this problem.
You could introduce the problem on an interactive whiteboard or data projector but it would be helpful for children to have a copy of this sheet in pairs and to work together so that they are able to talk through their ideas with a partner. Scissors and sticky tape would be
useful!
Some children will relish the challenge of discovering for themselves which shapes have been used but some may work better knowing which they were to find. The shapes are: a cube, cuboid, tetrahedron, square pyramid, pentagonal pyramid, hexagonal pyramid, triangular prism, pentagonal prism, trapezoid prism.
Key questions
How do you think these two pieces could fit together?
Which piece could go with this one?
What shape are the faces on a ...?