Copyright © University of Cambridge. All rights reserved.
'Tilted Squares' printed from https://nrich.maths.org/
Show menu
Tilted Squares printable sheet
It's easy to work out the areas of squares drawn on a grid if they are oriented in the usual way:
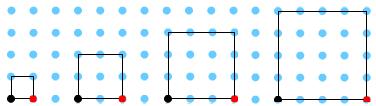
Can you find a quick and easy method to work out the areas of tilted squares?
Here are some squares with a tilt of 1:
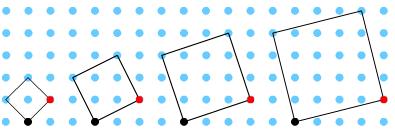
See the hint for suggested ways to calculate their areas.
Notice anything special about their areas?
Can you predict the areas of other squares with a tilt of 1?
What about squares with a tilt of 2? Or 3? Or 4? Or...?
Notice anything interesting?
Can you make any conjectures about the areas of tilted squares?
Can you prove your conjectures?
You might like to use the interactivity below to help you to draw tilted squares.
Full Screen tablet/mobile friendly version