Changing places
Problem
A four by four square grid contains fifteen counters with the bottom left hand square empty. The counter in the top right hand square is red and the rest are blue. The aim is to slide the red counter from its starting position to the bottom left hand corner in the least number of moves. You may only slide a counter into an empty square by moving it up, down, left or right but not diagonally.

Explore a four by four array. How many moves did you take to move the red counter to HOME (pink square)?
Can you do it in fewer moves? What is the least number of moves you can do it in?
Try a smaller array. How many moves did you take to move the red counter to HOME?
Try a larger array. What is the least number of moves you can do it in?
Have you a strategy for moving down each array?
On which move does the red counter make its first move?
On which moves does the red counter make its other moves?
Can you predict the number of moves that the red counter makes on the way HOME?
Why is the least number of moves ALWAYS odd?
Can you predict what the least number of moves will be for any square array?
Can you explain why YOUR rule works?
You can take this further by considering similar ideas using rectangular arrays or in three dimensions.
Getting Started
Once started on the journey home why is every third move important?
What is special about those counters that don't move?
Student Solutions
| Array | Moves |
| 2x2 | 5 |
| 3x3 | 13 |
| 4x4 | 21 |
| 5x5 |
29
|
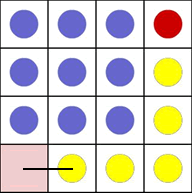
b) Now the red counter can move one place down:
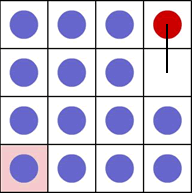
c) there is a series of repeated moves from now on:
There is a pattern which means that the red counter will move every third go, so that the red counter travels around the diagonal of the array.
In the figure below the path of the red counter from the last position, to home is represented.
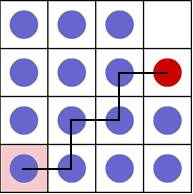
Overall, from this position, the red counter moves n - 2 squares down and n - 1 squares across. So we have:
n - 1 + n - 2 =2n - 3
Each time the red counter moves, two blue counters have to be moved to fill the empty space and create a new one that the red counter can move into. So, we obtain:
3(2n- 3).
Now, adding all the results to calculate the total number of moves:
(2n -3) + 1 + 3(2n -3) = 2n -3 + 1 + 6n -9 = 8n -11
Which matches the prediction.
Andrei also noted that the number of moves is always odd because 8n is always even and 11 is odd. For the 4x4 array, the red counter makes its moves on moves 6, 9, 12, 15, 18 and 21.
For the rectangular case, a similar strategy can be used.
Suppose the rectangle has $m$ rows and $n$ columns, with $m> n$.
First of all, we need $m + n - 3$ moves to get the space to next to the red counter. Then, we need use one move to put the red counter in this space.
We can then move $(n-1)$ squares down and $(n-1)$ across, using three moves per squareas before.
Now we must move down the last $(m-n-1)$ squares. This takes 5 moves for each square, as we do not alternate between horizontal and vertical moves. Adding all this up, the total number of moves needed is $$n + m - 3 + 1 + 2 \times 3(n-1) + 5(n-m-1) = 2n + 6m - 13$$
