Why do this problem?

This problem addresses a difficulty that many children experience with the numbers from ten to twenty. The 'teens' often cause more trouble than other decades up to 100 in English because of the irregularity of the language used. By focusing on creating the numbers from 11 to 19 using 10 and adding a single digit number, the problem gives an opportunity to practise building these numbers from one ten and different numbers of ones (the reverse of partitioning using place value). 

By including three different children's starting points, the aim is to encourage learners to be curious about multiple approaches to a task. By reflecting on different ways of solving the problem and talking about them, learners can begin to appreciate the problem-solving journey and not just the answer.

Possible approach

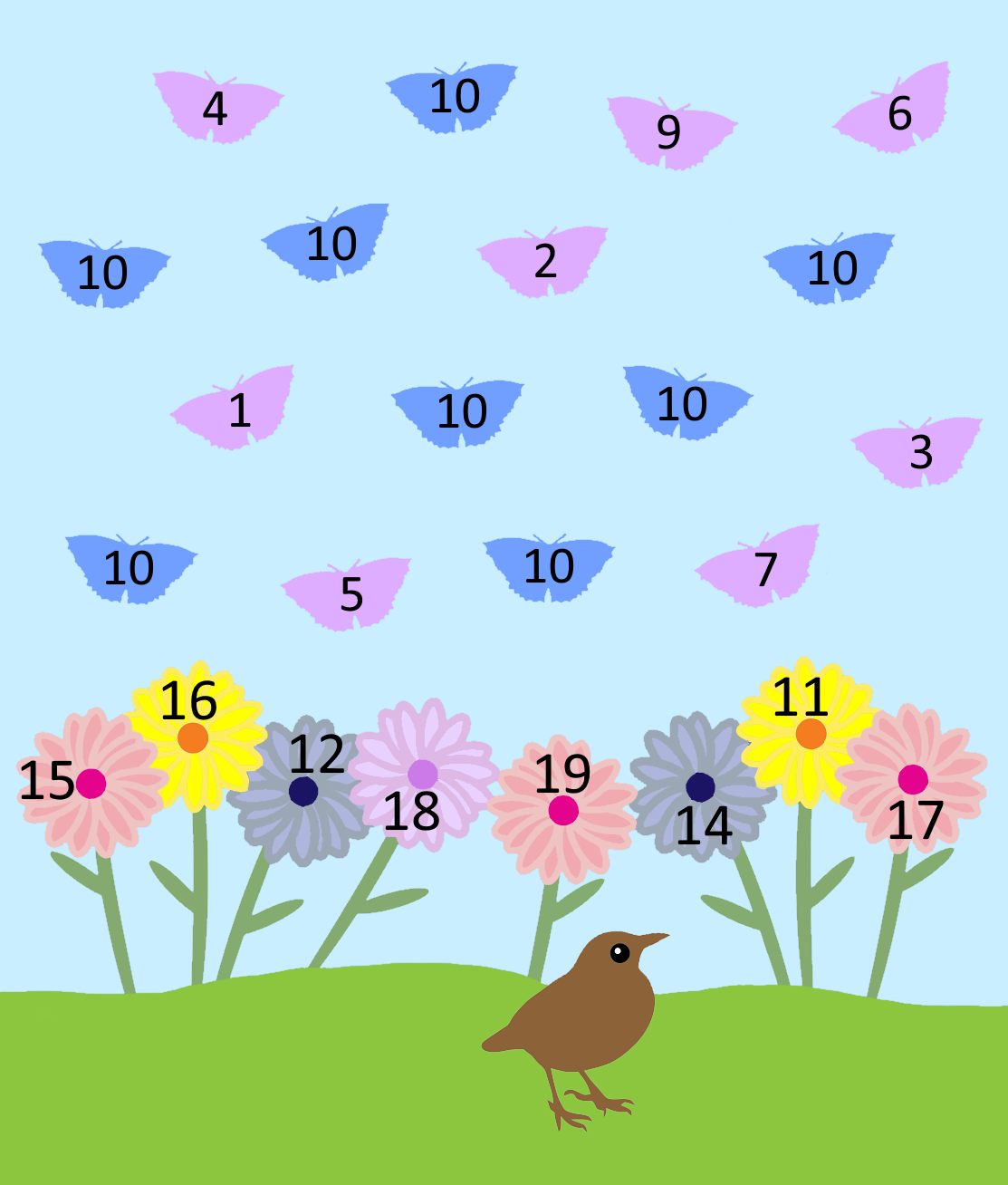
Show the image of the butterflies and flowers to the group and invite children to think about what they see. Give them YOYO time (You On Your Own) before suggesting they talk to a partner. Gather suggestions from the whole group, making sure all comments are valued, even if they appear to be non-mathematical in nature! Encourage other learners to comment on or question their peers' suggestions so that everyone feels involved.  

Once you feel you have established enough information, pose the question orally: "Can you find two butterflies to go on each flower so that the butterfly numbers add to the flower number?". Give children time to work on the task in pairs. Some butterfly and flower cards could be printed and laminated to be used by children - this set contains more numbers than are used in the task so you can choose some to leave out as needed. (They can also be useful as a set of cards for matching activities more generally.)

When everyone has found at least a few butterfly and flower groups, draw the class together and explain that you're now going to focus on how they have approached the problem. (You might like to reassure them that there will be more time to complete the task later.) It might be that you can draw on the methods that different pairs of children in the class have used, or you could share the three alternative approaches described in the problem as Zac's, Mona's and Anita's methods. Invite everyone to look at each method and understand it, before facilitating a general discussion about the different approaches. Did any pair use one of these methods? What do they like about each? What do they not like?

Key questions

What can you say about the picture?
How might you start?
What do you get if you choose two butterflies and add them together? What could you do now?

Possible extension

The cards could be used to make other pairs or sets of numbers that total to different target numbers. Multiple sets of the cards will increase the number of possible solutions.

Possible support

When children are counting together make sure that the 'teens' are well differentiated from the 'tens', for example, that 'sixteen' is well differentiated from 'sixty'.