Squirty
Using a ruler, pencil and compasses only, it is possible to construct a square inside any triangle so that all four vertices touch the sides of the triangle.
Problem
Using a ruler and compass only, it is possible to construct a square in any triangle so that one side of the square rests on one side of the triangle, and the other two vertices of the square touch the other two sides of the triangle:
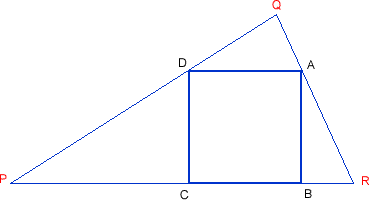
Can you find a way to construct the square, for any triangle?
Can you explain why your method works?
Getting Started
Can you draw a square ABCD with BC on the base PR of the triangle and the vertex D on the side PQ using ruler and compasses?
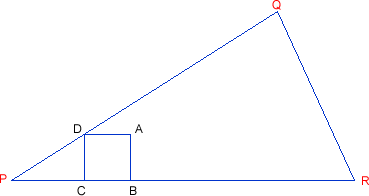
What happens to the point A as you enlarge the square? The interactivity may help. Move Q to specify your triangle, and then move D to enlarge the square.
How can you use this to help you draw the square you require?
Student Solutions
Thanks to Andrei of School 205 Bucharest for this well explained solution.
- First, I drew a line $HG$, perpendicular on $P$, and a line through H, parallel with $PR$.
- On it, I took a segment $HE$ of the same length with $HO$.
- Then I finished drawing the square $HEFO$, drawing $EF$ perpendicular on $PR$. The line PE intersects $QR$ in $A$.
- From $A$ I drew a parallel to $PR$ (let the intersection point with $PQ$ be $D$), and a perpendicular to $PR$ (let the intersection point with $PR$ be $B$).
- This way I found 3 vertices of the rectangle $ABCD$, and I finished the rectangle finding the vertex $C$ on $PR$, so that $CD$ is perpendicular to $PR$.
The rectangle $ABCD$ is a square because:- Triangles $PEF$ and $PAB$ are similar, they are both right-angled triangles, with a common angle. The similarity ratio is: $${{PE}\over{PA}} = {{EF} \over {AB}}$$ Triangles $PEH$ and $PAD$ are similar, because angles $PEH$ and $PAD$ are equal and $HPE$ is a common angle. The similarity ratio $$\frac{PE}{PA} = \frac{HE}{AD}$$ From $(1)$ and $(2)$ $$ \frac{AB}{EF} = \frac{AD}{HE}$$ As $HE=EF$ (sides of a square) Therefore $ AB =AD$ $ ABCD$ is a rectangle with two adjacent sides equal
Therefore $ ABCD$ is a square.
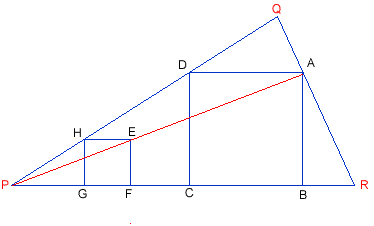
Now, the construction of the inscribed square must be done in the following steps:
- Choose a point $H$ on side $PQ$, near $P$
- Draw line $HG$, perpendicular on $PR$
- Take the distance $HG$ as the compass distance, and draw a circle arc, with centre $G$. $F$ is the point of intersection of this arc with $PR$.
- Construct two circle arcs with centres $F$ and $H$ (with the same radius as before). Their intersection is point $E$, and $EFGH$ is a square.
- Draw line $PE$. Let the intersection point of this line with side $QR$ be $A$.
- Draw from $A$ parallel to $EF$ and $HE$. Their intersections with $PR$ and $QP$ are points $B$ and $D$ respectively.
- Draw from $D$ a parallel to $AB$. Its intersection with $PR$ is $C$.
- $ABCD$ is the square to be found.
Teachers' Resources
Why do this problem
This activity involves problem solving with the restriction of traditional instruments: straight edge (i.e. an unmarked ruler) and compass. Tackling problems like this often involves working out what the task is asking for, doing something which might help but isn't the whole solution, reviewing the result of that to see what might be there to be noticed, and then using that observation to close the task. Along the way students might develop a deeper appreciation of the things they thought they already knew and could do easily.
Possible approach
This printable worksheet may be useful: Squirty.
Start the group off with the task of drawing a square of any size using only a ruler and compasses. There's plenty to challenge understanding just in that.
Next, ask each student draw a triangle, pointing out that because they can each draw the triangle they choose, what follows will be an exploration of any triangle.
Allow some discussion to establish that every student appreciates the task and that many 'first thoughts' about the task can be shared.
Pursue each suggestion, discussing these together as a group but with each student actually drawing for themselves. Exploring suggestions even if they do not lead to a solution can deepen understanding, and skipping this process could considerably reduce the value of the activity.
If a prompt towards something fruitful is needed, point out that partially meeting criteria can sometimes be helpful in the problem-solving process. This is a form of working systematically to explore the different constraints separately. In this case, students could try to create a square, based on one side, but where only one of the 'top' corners touches one of the other two sides of the triangle. Ask students then to draw another such square for the same triangle, and another. Drawing several of these may help students to think about the special one of this set that touches both sides.
Take time to let students notice how they create their squares. How they choose the base or the 'touch point' and from that go on to create the rest of the square. Once they have three or four squares invite them to stand back, take a look and then share what they notice.
At this point students may notice that for all these squares the 'top' corners that do not touch a side of the triangle seem to lie on a straight line. You could share the interactive in the Getting started section to support discussion of this.
It may be tempting at this point to assume all the work has been done, but encourage students to think carefully about how they would use what they have noticed to construct the square that meets all the conditions in the problem and articulate this. For example, can they describe the complete procedure from any starting triangle, and how would they convince someone else that that they have constructed a square meeting the conditions, not just a rectangle?
This is a relatively challenging task using ruler and compass, so it is worth taking the time to allow students to appreciate what kind of constraint 'ruler and compasses' imposes.
'Ruler' means that points can be joined and the line continued indefinitely from both ends, and 'compasses' means that a length can be picked up and transferred somewhere else.
It may also be worth allowing time for discussion to wander into methods which depart from the ruler and compass constraint.
In an alternative approach, students could also use the GeoGebra Geometry calculator to explore the problem, but make sure they think about whether the tools the are using relate to ruler and compass constructions.
Key questions
- Can you draw a square using only a straight edge and a pair of compasses ?
- What, in your own words, is the challenge or task here ?
- How might you start on that ? Can you do it 'straight off'' ?
- How can you use that to get the square you want ?
Possible support
Focus on creating squares just using ruler and compasses constructions.
Possible extension
ZigZag explores more of what makes a square.
These further suggestions may help to foster a classroom culture that 'plays' with compasses and sparks with geometric reasoning and insight.
Here's a couple of nice problems to start discussion and play.
- If I only have the three mid-points from the sides of a triangle can I recreate the triangle? See Triangle midpoints
- If I only have the centres of three circles where each circle touches the other two can I recreate the circles.
As before, these tasks are to use ruler and compasses, but do allow the discussion to wander into methods which depart from that constraint.
