 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Break it Up!



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everybody who sent in their solutions to this problem. We received lots of good ideas about the number of different ways of doing this, but most children found it tricky to create a convincing argument for why their ideas would always be true.
Ryan from Kong Hwa School in Singapore tried breaking up a few different sticks of cubes:
There are 6 ways to separate 7 cubes. There will be 7 ways to separate 8 cubes, 4 ways to separate 5 cubes and 19 ways to separate 20 cubes.
Thomas and Rosa from South Darley CE Primary School had a go at this task. Their teacher wrote to tell us:
Thomas and Rosa worked brilliantly together to find out how many ways there were to break 7 cubes and thought the rule might be that there is one less break than the number of cubes. They tested it with other numbers of cubes and found they were right.
Here is a picture of their recording:

It looks like they have worked very systematically, well done!
Natalie from North London Collegiate School in the UK took this pattern and wrote it as a general rule, like Rosa and Thomas:
I have discovered that the number of ways have to be one less than the number of cubes.
Well done to both of you for investigating this pattern. We had similar solutions sent in by: Siena, Samar and Jade from Westridge School; Bella from North London Collegiate School; Hasan, Jana and Mohammed from Abdulrahman Kanoo International School in Bahrain; George and Kai from Twyford School in the UK; Lucas and Ryan from Kingswood College in Australia; and Hope, Ellie and Bowen. Thank you all for sending in your solutions - unfortunately we don't have space to feature all of them here.
Teija from Pierrepont Gamston Primary School in the UK explained why the number of ways of splitting the blocks must always be one less than the number of blocks:
To answer the ‘Break it up!’ puzzle, I first estimated what I thought and then tested it. After working out the possibilities for different numbers such as:
5 blocks = 4
6 blocks = 5
7 blocks = 6
I realised that each answer was one less than the number of blocks used and asked myself ‘Why?’. I continued to work on more answers and my hypothesis remained the same. Then I thought about the sums and how I was splitting them, e.g.
6+1
5+2
4+3
3+4
2+5
1+6
Then I saw that there was one missing: 7+0/0+7 and thought about how that is because, if you tried it with blocks, you would not be splitting the line so that means that there would only be 6 possibilities because the seventh does not follow the rules to form two pieces. This is the same for all numbers.
Well done, Teija - this is a really convincing explanation for why the number of possibilities is always one less than the number of blocks. Prayaan from King's College Junior School explained the pattern in a different way by thinking about the joins between each brick:
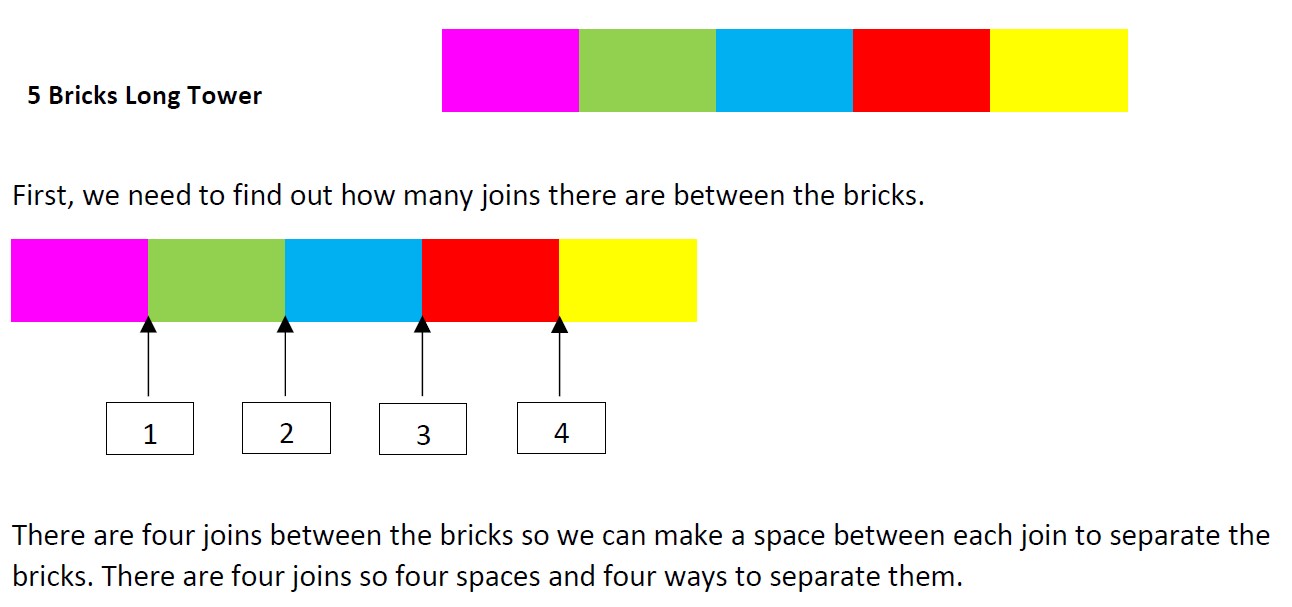
Prayaan used this idea to come up with the general rule:
The answer will always be one less than the number of bricks because the joins are one less. Using this logic, we can now predict the number of possible combinations of any number of bricks. Just subtract one!
Good explanation, Prayaan!
Some children decided that 1+6 and 6+1 should count as the same arrangement. Haleema from Pierrepont Gamston Primary School sent in this explanation:
With seven cubes (1 and 6, 2 and 5, 3 and 4) and with six cubes (1 and 5, 2 and 4, 3 and 3), there are three possible solutions and with eight cubes, there are four resolutions. They are 1 and 7, 2 and 6, 3 and 5 and 4 and 4. For the answer for five cubes, I predicted two solutions (1 and 4, 2 and 3) and after working it out, I discovered that I was right. There are also ten ways for 20 cubes. I have possibly found a pattern in how many solutions there are for every amount of cubes. For an even amount of cubes, there are half of that number of solutions. For example, take 50 cubes. You will most likely find that there are 25 solutions. Half of 50 is 25. When there is an odd number though, you half it and take away 0.5. Take 15. Half of that is 7.5. Take away 0.5 and you have seven solutions.
Daisy, Eshal and Emilia from Halstead Preparatory School sent in the following picture and explanation. They found a slightly different way of describing the pattern:

We noticed that when the number of cubes is odd, you take away one and then divide by two in order to find the number of breaks. If it is even you just divide by two.
Our prediction is that for all the even numbers of cubes you have to divide by 2 and for all the odd numbers of cubes you take away 1 and then divide by 2. This works because you can only change the amount of cubes on each side counting down to half way because otherwise you will be repeating numbers.
Well done to all of you for your clear explanations. We also had similar solutions sent in by Claire from Westridge School and by Dhruv from St. Anne's RC Primary School in the UK.
Ci Hui Minh Ngoc from Kong Hwa School in Singapore thought about what would happen if the cubes were split into three pieces. Have a think about this for yourself first. Are there any patterns in the numbers of combinations? Once you've spent some time thinking about this, have a look at Ci Hui Minh Ngoc's full solution to see the patterns they spotted.