Copyright © University of Cambridge. All rights reserved.
'Up and Down Staircases' printed from https://nrich.maths.org/
Show menu
We had some good solutions coming from Peak School Hong Kong. Firstly Ethan wrote the following and sent in a picture:
One step up takes one block.
Two steps take four blocks.
Five steps take twenty-five blocks.
"A" steps will take "A"squared blocks (A x A).
So the rule is any number of steps times itself equals the number of blocks you use.

Pradeep, Victoria, Anaya, Dorika, Anna, Marcus, Christiana and Ian said similar things to arrive at the same findings. Holly also from the same school in Hong Kong sent in this detailed explanation:
The first time there is 1 block; 1 step up and 1 step down.
Then there are 4 blocks; 2 steps up and 2 steps down. Altogether the blocks equal 4. (3+1=4) Since 1 double is 2 and 3-1=2 we should try adding 2 each time. Then it would get to this ...
I
III
IIIII
IIIIIII
IIIIIIIII
This makes perfect sense because 1+3=4 which is the top two lines as 4 was the answer to the second time the blocks were built. 4+5=9. This one would be the third time. 9+7=16. 16 would be the fourth time. And lastly, 16+9=25.
The fifth time (which is the answer) would look like this on the form of steps...
I 1
III 3
IIIII 5
IIIIIII 7
IIIIIIIII 9
This answer has five steps up and five steps down just like the question. That comes to the answer which is 25.
Well done all you pupils from Peak School.
We also had many responses from Holy Trinity School, Halstead. Here is Olivia, Maisy and Amelia's response:
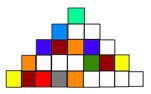
The amount of blocks that would be needed for a staircase going 5 steps up and 5 steps going down would be 25. Unless you wanted a flimsy stair case with no inside then it would need 9 blocks to form the base (as shown on the diagram above).
If we had to build a staircase with any numbered steps (for example 8) we would start to think about how many blocks we needed. So we thought that the staircase with 8 steps up and steps down would have 64 blocks in total so that we found out these numbers for the staircase are square numbers.
If you do any other number (for example 10) you times that number by itself which is 100 so then you do 100 blocks.
Kaci-Mai, Mia and Ben, also from Holy Trinity, sent in the following:
We looked at how we could make a staircase out of 1 block so it would be a step up and a step down and first we didn't seem so confident about doing this but then we read the instructions and we kind of got the hang of it.
The next step was doing a staircase made of 4 blocks and when we read that there were only four blocks to use we didn't get how you could do it. After that we started to think about how we could do it, until we realised that it would make 2 steps up and 2 steps down.
We had to do 5 steps up and 5 steps down, this time we knew what to do so we just started by doing 5 up and 5 down with gaps in between the blocks. After that we filled in all the gaps with blocks so it will support the blocks above. As we looked at the staircase we realised that there were twenty-five blocks which is five times five.
The last step was when we had to do 7 up and 7 down. The difference is that we found out how many blocks more there was 2 steps up and 2 steps down compared to the one step up and one step down. Then we put blocks underneath so it can support the blocks above. We counted all the blocks together and it made 49.
Then we tried a 10 up and 10 down staircase we did ten across the bottom, then 9 and kept going till we got to the top, then we counted all of them together and it equals 100 blocks staircase.
These pupils, also from Holy Trinity, sent in good solutions: Declan, Harrison, and Dominic; Spencer, Freddie, Jack and Ben; Oliver, Finlay and Levi; Yildiz, Holly and Jessica; Eleanor, Sienna and Alex; Elizabeth, Katie and Tobie. Here's the one from Lucy, Jack and Sonny:
First we read the instructions to help us know what we needed to do to solve the problem. So we figured out we needed to draw on a whiteboard or use multi-link and build a pyramid because the question said find out how many blocks are in the pyramid with five steps up and down. The best and clearest way is probably to use multi-link in our opinion. Nine blocks should be in line with each
other at the bottom of the pyramid.
Now we built the rest of the pyramid with five steps up and five steps down, all the blocks should be in line with each other one on top of each other. Once you have done that count all the blocks inside the pyramid and your answer should come to twenty-five (25).
After that we tried to do seven and ten to see if there was a trick then we found out if you look closely and think about you answers you will notice a trick, and the trick is however many blocks is on one side of the pyramid you times that by itself this trick is called square numbers. This happens on every number you use but the trick only works when you use one side of the pyramid and only
times that number by itself.
Now try and do seven blocks up and down the staircase in your mind and if you get the answer of 49 you would now know a quicker way to work out the staircase process. We found out the trick because we did one block up and down then two blocks then five by then we could see a pattern so we tried ten and it worked so that is are explanation on how we figured out this problem.
Evie and Oscar from Harrison Primary School, Fareham sent in this response:
To find a solution to the 5 step challenge our first step was to draw a diagram to see the number of cubes.
We then worked out how many cubes would be needed for a staircase with 2, 3 and 4 stairs using the same type of diagram.
Next we put our data (our findings) into a bar chart to try and find a pattern between the number of cubes and steps. After seeing our data this way we saw the pattern and difference. We found that for the number of steps there were, if you squared the number of steps you got the number of cubes you would to use. Consequently, the algebraic formula would be n².
This made us realise how much could be done with algebra and how useful it is.
Our first Solution from North Cyprus came from Mr Atkinson English School of Kyrenia:
My class tried this. Here is what they found:
25 blocks make an up-and-down staircase with 5 steps up and 5 steps down.
NxN blocks make an up-and-down staircase with N steps up and N steps down. (Anna)
We multiply the number of steps up by the number of steps down. (Deniz G and Deniz K)
They then tested this with larger numbers to check that it worked.
Here is their picture that shows how it's to do with square numbers:
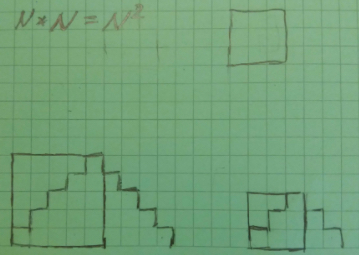
This final solution from North Cyprus is particularly helpful as it explains WHY the squaring pattern occurs.
Well done all of you and thanks for your ideas as to how to solve this challenge.