Picturing Triangle Numbers

In this problem we are going to consider triangle numbers.

Your aim is to find a method for working out the value of any triangle number.
You will then be able to use your method to identify quickly whether numbers are triangular.

Triangle numbers can be represented by a triangular array of squares.

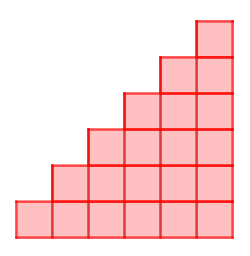
Imagine two copies of a triangular array of squares. Can you picture how to fit them together to make a rectangle? What is special about the dimensions of your rectangle?

Use the activity below to test your ideas.

What do you notice about doubling triangle numbers?
Experiment with different triangle numbers and explain what is special about the rectangles made from two identical triangle numbers.

Can you write down the dimensions of the rectangle made from two copies of the 250th triangle number? Can you use this to work out the 250th triangle number?

Check - your answer should be somewhere in this list: $29184, 31375, 586594, 908475, 2092035$

Have you a strategy for finding any triangle number?
If your strategy works, write down your method as clearly as you can.

Consider the following numbers: $4851, 6214, 3655, 7626, 8656$.

Which are triangle numbers?

Describe a quick way of deciding.

Do any triangle numbers end $000$?

You may wish to try the problems Mystic Rose and Handshakes. Can you see why we chose to publish these three problems together?

You may also be interested in reading the article Clever Carl, the story of a young mathematician who came up with an efficient method for adding lots of consecutive numbers.