Anti-magic square
Problem
A 4 by 4 "anti-magic square" is an arrangement of the numbers 1 to 16 in a square, so that the totals of each of the four rows and four columns and two main diagonals are ten consecutive numbers in some order.
The diagram shows an incomplete anti-magic square.
| 4 | 5 | 7 | 14 |
| 6 | 13 | 3 | |
| 11 | 12 | 9 | |
| 10 |
Can you fill in the missing numbers (1, 2, 8, 15 and 16) to complete it?
Click to reveal an interactivity that you may wish to use to help you solve the problem.
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
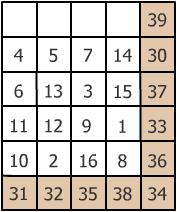
The totals of the top row and completed main diagonal are 30 and 39 respectively and therefore the 10 consecutive numbers in question must be 30 to 39 inclusive.
The number in the bottom right hand corner must be 1, 2, 8, 15 or 16. Taking 1 and 2 the completed diagonal would add up to less than 30 whilst 15 and 16 produces a number greater than 39. Hence 8 must go in the bottom right hand corner. It now follows that the last digit in the second row must be 15 since if 15 is placed in any one of the other three vacant squares, we get a total of 45 in the second column, 34 in the third column (same as the diagonal) and 47 in the third row (too big). We are now left with 1, 2 and 16. End third row must be 1 to make the column less than 39 (38) and the row total 33. This leaves 2 and 16 making the forth row total. 16 cannot go in column 2 as this makes a total greater than 39.
