 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Star Sum



- Problem
- Solutions
Answer: 13
Using algebra to compare the letters
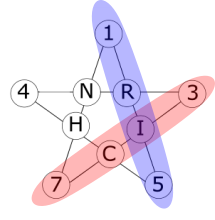
I + R + 6 = I + C + 10
$\therefore$ R + 6 = C + 10
$\therefore$ R is 4 more than C
But that is only possible if R = 13 (and C = 9)
Using reasoning
1 + 3 + 5 + 7 + 9 + 10 + 11 + 12 + 13 = 75
Each number is on 2 lines so the lines add up to 75$\times$2 = 150
Five lines $\therefore$ 30 per line.
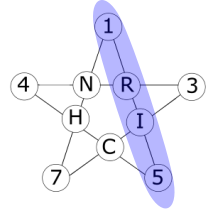
1 + R + I + 5 = 30 $\Rightarrow$ R + I = 24
R and I are 11 and 13
If R = 11:
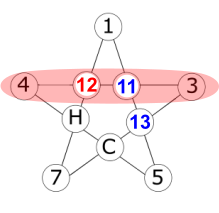
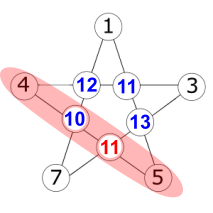 Can't have 11 twice
Can't have 11 twice
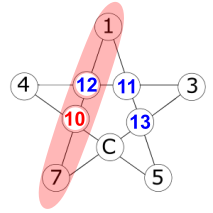
If R = 13:
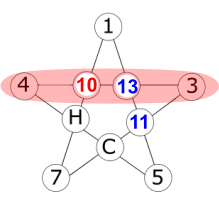
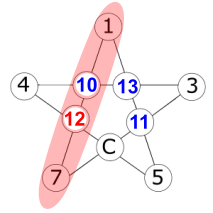
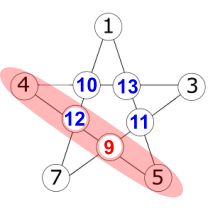
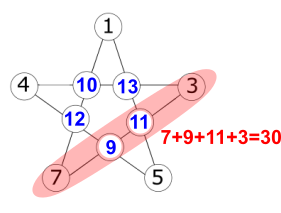 So R = 13
So R = 13
Alternatively, using algebra and equating the sum of each line
We are told that the sum of each line is equal. Therefore $1+R+I+5, 4+N+R+3, 7+H+N+1, 5+C+H+4$ and $3+I+C+7$ are all equal.
Combining the equations with a common term in turn gives:
$1+R+I+5=4+N+R+3⇒6+I=7+N⇒I=N+1$
$4+N+R+3=7+H+N+1⇒7+R=8+H⇒R=H+1$
$7+H+N+1=5+C+H+4⇒8+N=9+C⇒N=C+1$
$5+C+H+4=3+I+C+7⇒9+H=10+I⇒H=I+1$
$1+R+I+5=3+I+C+7⇒6+R=10+C⇒R=C+4$
The last of these equations is a good check to make sure that the results of the others work.
This means that, in increasing order, adding one each time, the numbers are $C$, $N$, $I$, $H$, $R$.
Therefore, $R$ is the largest number, so $R=13$ (and $H=12, I=11, N=10$ and $C=9$, which is $4$ less that $R$ so is correct).