This problem consolidates children's understanding of halving in a spatial context and will help them to develop their powers of visualisation.

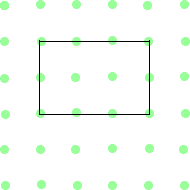
A precursor to this activity might be to show the group a square and ask them to split it in half in their "mind's eye". By discussing where they have imagined the "cutting line", the children will discover that there is more than one way to do this. From this point, you can talk about whether or not the two halves look the same each time. It is important pupils are clear that, in this problem, the halves must look identical to each other.

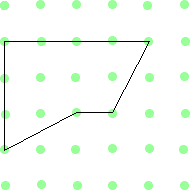
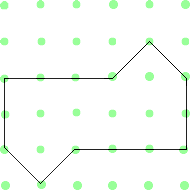
It may be useful for the pupils to have this sheet of the shapes. Alternatively, they could use a pegboard or geoboard to try out their ideas.

In the plenary, you could focus on how they know the two parts they have created are definitely identical halves. This might involve children describing turning one part so that it fits on top of the other and some learners might want to practically do this by cutting out the two parts of each shape.

Where could you try splitting the shape?

How do you know those two parts are identical halves?

What could we do to check?

Using the same size grid, children could create examples of shapes for a partner to split in half. This problem offers some more shapes which children could try.

Pupils could try Halving before having a go at this problem.