Circle Box
Problem
Four circles of diameter 1 unit fit easily enough in a square of side 2 , but what is the smallest square into which we can fit 3 circles of diameter 1 unit?
Getting Started
Join the centres of the circles.
Consider symmetry then use Pythagoras and a little trigonometry.
Student Solutions
Many thanks to Hannah of The School of St Helen and St Katherine for submitting this solution. Very well done Hannah.
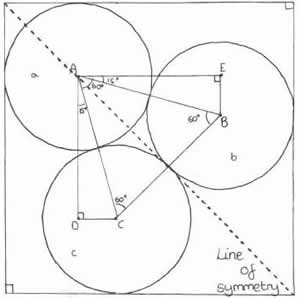
Looking at the diagram of the problem; let the top circle be a, the slightly lower one be b and the bottom one be
c and their centres A, B and C.
Draw a horizontal line to the left of C and extend it to the edge of the square.
Now draw a vertical line down from A and call the point where it meets the line you have just drawn D so that angle ADC = $ 90^o $
It is also worth noting that triangle ABC is equilateral and the whole box has a line of symmetry running from the top left hand corner of the square to the bottom right.
The angle DAE (on diagram) is $ 90^o $ and the angle CAB is $ 60^o $ because it is an equilateral triangle. Therefore angle DAC + angle EAB equals $ 30^o; (90^o - 60^o) $ meaning that angle DAC is $ 15^o $; as it equals EAB.
Now we can use trigonometry to work out the length AD (from A, vertically down to D). Using the triangle ADC, the hypotenuse of which is 1cm (two radii), ($ 90^o \times 1 = 0.965...$)
From C to the base of the square is 0.5cm (radius), which is equal to the distance from D to the base of the square. From A to the top of the square is also 0.5cm (radius)and you can add these two values on to AD to get a side of the square.
Therefore one side of the square $= 0.5+0.5 (a+c$ radii$)+0.965... =1.966$ cm(3d.p.)
Teachers' Resources
The arrangement of the circles in the diagram is worthy of some discussion. How do we know the surrounding rectangle is a square and that the arrangement gives us the smallest square?