Two circles of equal radius touch at the point P. One circle is fixed whilst the other moves, rolling without slipping, all the way round.

How many times does the moving coin revolve before returning to P?

What happens if the radius of the moving circle is half that of the fixed circle? Can you generalise your results further?

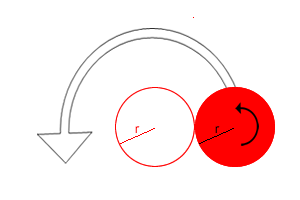
You may wish to use the GeoGebra interactivity below to test out your conjectures.

Here are two related problems you might like to take a look at:
Rolling Around
Is There a Theorem?