Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Flower
Age 16 to 18
Challenge Level 





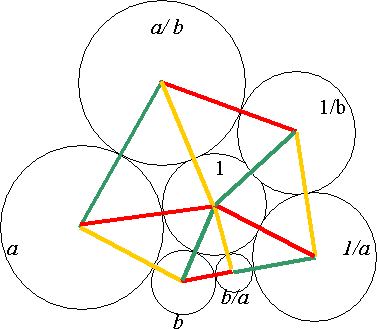
You are given a circle of radius 1 unit and two circles of radius $a$ and $b$ which touch each other and also touch the unit circle. Prove that you can always draw a 'flower' with six petals (as in the sketch) with the unit circle in the middle, and six circles around it having radii $a$, $b$, $b/a$, $1/a$, $1/b$ and $a/b$, such that each outer circle touches the unit circle and the two circles on either side of it.
[Note: this diagram is not drawn accurately. Drawing your own more accurate diagram may help you to do the question.]