Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Lunar Angles
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Here is an excellent solution from Andrei from School No. 205,
Bucharest, Romania.
I divided the solution into two parts: the demonstration of the congruence of angles, and the demonstration that the three angles add up to $180^o$.
1. Congruence of angles in a lune
Let $O_1$ and $O_2$ be the centres of two circles, $A$ and $B$ the intersection points and $M$ and $N$ the intersections of the tangents to these two circles. I observed that triangles $O_1AO_2$ and $O_1BO_2$ are congruent, because they have a common side $O_1O_2$, and the other two sides are radii in the two circles. So, angle $O_1AO_2$ and $O_1BO_2$ are equal to say $\theta$. A tangent to a circle and the radius to the point of contact are perpendicular so $\angle MAO_2 = \angle NAO_1 =\angle MBO_2 = \angle NBO_1 = 90^o$. Hence $\angle O_1AM = \angle O_2AN =\angle O_1BM =\angle = \angle O_2BAN = \theta - 90^o$. So, $\angle MAN = \angle MBN$.
2. Let $O_1$, $O_2$ and $O_3$ be the centres of the three circles respectively, D the point common to all three circles, and $T_1T_1'$, $T_2T_2'$, $T_3T_3'$ the three tangents. In my figure the radius and the tangent to circle 1 are in red, to circle 2 in blue and to circle 3 in green respectively.
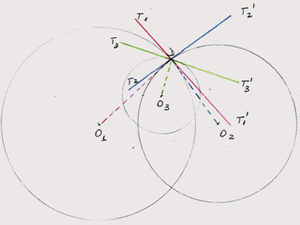
From the previous point, I see that angle $\alpha$ has the same measure with angle $T_2DT_1'$ and to the angle $T_1DT_2'$ (the last two being vertically opposite angles).
In the same manner I found: $\beta = \angle T_1'DT_3' =\angle T_1DT_3$ and $\gamma = \angle T_3DT_2 = \angle T_3'DT2'$. \par This way, it is easy to see that the three angles add up to $180^o$: $\alpha + \beta + \gamma = T_2DT_1' + T_1'DT_3' + T_3'DT_2' = T_2DT_2' = 180^o$. \par For the second case, I follow exactly the same steps.
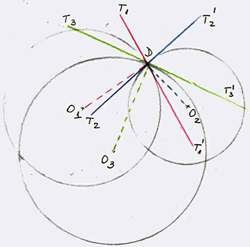
I find $\alpha = \angle T_2DT_1'$, $\beta = \angle T_2'DT_3' = \angle T_2DT_3$ and $\gamma \angle T_3DT_1 = \angle T_3'DT_1'$.
The result is the same, i.e. that in this case the three angles add up to $180^o$ again.
I divided the solution into two parts: the demonstration of the congruence of angles, and the demonstration that the three angles add up to $180^o$.
1. Congruence of angles in a lune
Let $O_1$ and $O_2$ be the centres of two circles, $A$ and $B$ the intersection points and $M$ and $N$ the intersections of the tangents to these two circles. I observed that triangles $O_1AO_2$ and $O_1BO_2$ are congruent, because they have a common side $O_1O_2$, and the other two sides are radii in the two circles. So, angle $O_1AO_2$ and $O_1BO_2$ are equal to say $\theta$. A tangent to a circle and the radius to the point of contact are perpendicular so $\angle MAO_2 = \angle NAO_1 =\angle MBO_2 = \angle NBO_1 = 90^o$. Hence $\angle O_1AM = \angle O_2AN =\angle O_1BM =\angle = \angle O_2BAN = \theta - 90^o$. So, $\angle MAN = \angle MBN$.
2. Let $O_1$, $O_2$ and $O_3$ be the centres of the three circles respectively, D the point common to all three circles, and $T_1T_1'$, $T_2T_2'$, $T_3T_3'$ the three tangents. In my figure the radius and the tangent to circle 1 are in red, to circle 2 in blue and to circle 3 in green respectively.

From the previous point, I see that angle $\alpha$ has the same measure with angle $T_2DT_1'$ and to the angle $T_1DT_2'$ (the last two being vertically opposite angles).
In the same manner I found: $\beta = \angle T_1'DT_3' =\angle T_1DT_3$ and $\gamma = \angle T_3DT_2 = \angle T_3'DT2'$. \par This way, it is easy to see that the three angles add up to $180^o$: $\alpha + \beta + \gamma = T_2DT_1' + T_1'DT_3' + T_3'DT_2' = T_2DT_2' = 180^o$. \par For the second case, I follow exactly the same steps.

I find $\alpha = \angle T_2DT_1'$, $\beta = \angle T_2'DT_3' = \angle T_2DT_3$ and $\gamma \angle T_3DT_1 = \angle T_3'DT_1'$.
The result is the same, i.e. that in this case the three angles add up to $180^o$ again.
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Logosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.