 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Circles in Circles



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This solution together with the diagram was sent in by Derek Wan, age 17 of Sha Tin College, Hong Kong
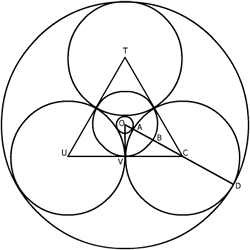
To find $OA=r_1$, $OB=r_2$ and $OD=r_3$ we must examine the diagram and make appropriate considerations. By dropping a perpendicular from $O$ to $V$, the midpoint of $UC$, as the radius is perpendicular to the tangent, we can find $OA = r_1$. Since triangle $TCU$ is equilateral $\angle TCU=60^o$ and $OC$ bisects $\angle TCU$ so $\angle OCV = 30^o$.
Since $OC=OA+AC$ $${CV\over OA+AC}={\sqrt 3 \over 2}$$ As $AC=CV=1$ and $OA=r_1$, $${1\over r_1+1} = {\sqrt 3 \over 2}$$ $$r_1+1 = {2\over \sqrt 3}$$ $$r_1 = {2\over \sqrt 3}-1$$ With $r_1$ we can find $r_2$ and $r_3$. Since $OV=r_2$, $CV=1$ and $\angle OCV=30^0$, $$r_2={1\over \sqrt 3}.$$ Since $OD=OA+AC+CD$, $$r_3={2\over \sqrt 3} - 1 + 1 + 1 = {2\over \sqrt 3} + 1.$$ Now $$r_1r_2 = \left({2\over \sqrt 3 }- 1\right )\left({2\over \sqrt 3} + 1\right )$$ $$\quad = {4\over 3} + {2\over \sqrt 3} - {2\over \sqrt 3} - 1$$ $$\quad = {1\over 3}$$ $$\quad = \left({1\over \sqrt 3}\right)^2$$ $$\quad = r_2^2$$