You need twelve counters and two ordinary $1$-$6$ dice for this activity.

Draw out a board like this (you may find that squared paper is useful!):

Or, you can print it off here: pdf .

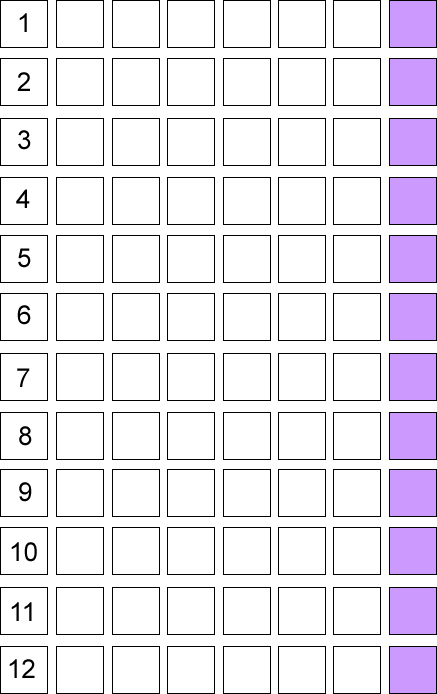
RULES

Place one of the twelve counters on each of the squares numbered $1$ to $12$.

Roll the dice and add together the two numbers shown.

Move the counter on that numbered square one box to the right.

Now roll the dice again and repeat this, each time moving the counter on that "row" one box to the right.

Which counter reaches the purple box first?

Is this what you would expect?

Play a few more times and make a note of which counter reaches the end of its row first.

Can you explain why you get these results?