This article was written following a conversation with a teacher of young children who was planning a unit of work on pattern. She bemoaned the fact that children enjoyed the work but to her it was repetitious because of the limitations of what could be done. I kept thinking about the comment and concluded that the problem with patterns is there is so much that can be done. In fact the whole curriculum could, and perhaps should, be organised around pattern.

We live in a universe of patterns.

So begins Ian Stewart's book Nature's Numbers, a fieldtrip that takes the reader sightseeing in the mathematical universe that is the world around us. It is interesting that Stewart sees fit to take his adult readers on that intriguing and important journey into pattern as he explores what mathematics is for and what it is about. Interesting because many teachers query why investigating pattern has such a central role in the mathematics' curriculum for younger explorers. In asking why pattern, what is it studied for and what is it about, we are actually asking about the role and purpose of mathematics itself.

Mathematics is the study of patterns. Studying pattern is an opportunity to observe, hypothesise, experiment, discover and create. By understanding regularities based on the data we gather we can predict what comes next, estimate if the same pattern will occur when variables are altered and begin to extend the pattern. Practical activities that allow us to construct knowledge for ourselves with all of the ingredients for a meaningful, thought provoking and mentally and physically engaging mathematics curriculum.

Study of pattern integrates both the strands of mathematics and a variety of curricular areas. We can use and extend skills and knowledge of number, measurement, geometry, data collection and statistics, probability and algebraic thinking. It allows us to bring together mathematics with music, visual art and craft, vocabulary building, creative writing and verbal communication, social studies, science and environmental studies, talent and technology. What better way to build a rich, developmentally appropriate curriculum for youngsters?

If we ask the youngest of learners, "What are patterns?", calling on their prior experiences and knowledge, they often use fabric, wallpaper, wrapping paper or building bricks to indicate their understanding. Somewhere is the idea of repeating over and over again. But, what are some of the pattern 'pieces' we can choose from so that we don't feel as though we are repeating the same instructional material over and over and over again?

Although used so frequently in early classrooms, we don't often connect the pattern of repeated sound and words in story, song and rhyme and relate it to maths. Is it a simple A, B pattern? An A, B, A, B pattern or more complex, perhaps with three or more elements. What symbols can be used to represent the pattern - can it be clapped, clicked, counted, drawn? Is the pattern generalisable - can we find other tunes, poems that have the same rhythm or beat? What will come next, what happens if we switch two of the elements, will A, A, B, B sound the same as B, B, A, A?

No fieldtrip into the local environment is complete without looking for the patterns that brighten and enliven our world. What patterns are present, are they from the natural or manmade world? What are the elements of pattern? What shapes do we see, how are colours used, do the patterns have meaning or purpose, how many varieties are there, how do they differ, what elements are the same? Looking at the overlapping tiles or wooden shingles on a roof we see a wide variety of patterns.

We see the same type of pattern in the leaves of certain plants, on the scales on fish and snakes and fir tree cones. They are not just pretty they are protection. Animals having overlapping body structures are flexible; they can curl up. We might not be able to see an armadillo first hand, but meal worms (known also as pill bugs and roly-polys) can be found easily in most damp outdoor environments. Looked at through a hand lens, the pattern of the overlapping structure can be seen.

A trick with overlapping playing cards demonstrates one of nature's fundamental laws. Overlap one card in a line on the next and flip the fist card laid down. All of the cards move and turn. Change to the pattern in one element of a system causes change and disruption to all elements of the system.

Typically we consider the elements of shape and colour, often colour simply emphasises shape. Tartans are created through the same basic element, repeated lines, intersecting. The variety is immense as the thickness and colour of lines alternate, as we see in books detailing Scottish clans and their tartans. We could be even more creative in designing our own tartans and clan history than the Celts were.

Some lines are not all that they seem. Zebras' stripes have pattern, but how can we describe it? The stripes are the fingerprints of the animal, each has its own unique pattern. They are an example of how the purpose of pattern comes into its own in the natural world. In the animal kingdom, like colour, they are signal friend or foe. The stripes of a zebra act to distort what the predators see. We could investigate the effect of different shapes in helping animals hide and keep safe.

Stripes, lines or bands of colour, can cause optical illusions. Here is an opportunity to investigate the causes after-images on the retina. Pattern and colour is seen to change as the speed of the motion increases. Colour wheels or discs made of lines, circles or coloured sectors can be stuck (masking tape works very well) on the end of a hand-held electric beater and observed as the speed increases. The results are fascinating.

Colours are nature's alarm clocks waking us up to the different and changing pattern in the seasons. Being able to read the pattern of the seasons was man's first way of measuring passing time. Recording daily changes in temperature, amount of sunshine, rainfall etc. provides children with an opportunity to develop ways to record, organise and retrieve, as well as interpret, use and display real data. Data, information that can be used to solve problems, is full of pattern and the purpose of analysing data is to enable people to predict and plan. We can do plenty of that with climate, weather and other seasonal data.

Motifs on buildings and in fabrics, in the trimmings and decorations that brighten our lives, often illustrate repeated patterns. We are surrounded by translational or rotational symmetry patterns. Look around: bottles in a rack, wallpaper and fabrics, borders and ribbons, fruit cut in half, letters of the alphabet and houses in the street. Mathematical vocabulary, sorting and classifying skills are developed and extended as attributes and properties of geometric shapes in these patterns are recognised and described.

Measurement, design and technology can be brought in as accumulated knowledge of pattern is applied. A motif can be designed, cut into polystyrene, lino or potato and printed on to large sheets of paper.

Wrapping gifts in your own paper makes it special. Why not wear your maths lesson? Children could cut their motif from pop-up sponge, which then swells in water, with fabric paint they can personalise a plain coloured tee shirt.

The questions to be asked are: how does the motif itself have pattern; how will the motif be used in a design; will it be repeated across the material; will the design be symmetrical? There is more than one form of symmetry and this is an ideal opportunity to discover the different types of pattern created by different symmetries. Do the shapes tessellate?

The questions to be asked are: how does the motif itself have pattern; how will the motif be used in a design; will it be repeated across the material; will the design be symmetrical? There is more than one form of symmetry and this is an ideal opportunity to discover the different types of pattern created by different symmetries. Do the shapes tessellate?

No study of pattern would be complete without regard to tessellation. Finding shapes that fit together without leaving gaps between them has long been a preferred way for people to add visual decoration to their built environment.

Mosaic and stained glass windows are the usual way to explore tessellations with young children, and the hexagon is the shape of choice.

As well as examining soccer balls and honeycombs, there are other hexagonal patterns to be explored. Try to arrange a set of the same sized coins so that they fit as tightly together as possible. Six of them will always cluster around the central one to form a shape similar to a honeycomb. What happens with different sized coins?

here is no doubt that the circle has a unique beauty. Concentric circles, those endless series of ripples and rings are fascinating. Investigating the pattern created when one or more stones are dropped into a pool allows children to dip into concepts of gravity, force, resistance, motion and surface tension. No nature fieldtrip is complete without investigating tree rings.

How do local species compare with a Giant Sequoia from Nevada which, through its rings, was found to be 3500 years old? What important history unfolded during those lifetimes? Why are some rings thicker than others, how can we know about the climate during the years the tree was alive?

Children are never too young to learn the value of tools in mathematics, especially for geometric constructions. Little hands may require some help and guidance with safety compasses, but the fascinating patterns they can create are worth the effort. Having children experiment to find out how, with a little help from their friends, they can turn a piece of string and pencil into a compass may produce a low-tech instrument but it is an exercise in lateral thinking.

Where else do we see concentric circles? On old records, compact disc surfaces? Well, yes to the first but no to the second. A strong magnifying lens will help the careful observer see that in fact the CD is made of millions of tiny dots arranged in tight spirals.

Spirals start at a central point and coil around. They are easily seen on nautilus shells and ammonite fossils, in springs and the threads of screws and the tight coils of tendrils on climbing plants. Is there a purpose to this natural and common manmade shape? If we look at and think about spiral staircase we begin to get a clue. They take up very little space and in some structures are very strong - springs are tight and tough!

Spirographs, whether the wheels of varying sizes or the newer battery operated pen style, allow youngsters to create neat and regular spiral shapes. Again, string, pencil and a friend to gently pull and shorten the string length, act together to make an admirable tool. If we pull out those magnifying lens again we will discover that spiders' webs also spiral out from the centre. Not what we expect!

What we probably expect to find in a web is a radial pattern, that is to say, one in which straight lines radiate from a central point. If not in a spider's web where do we see radial patters?

Where roads meet at a roundabout, on a dart board which is a combination of concentric circles and radial sections, in cactus spines where they meet the barrel and in flowers like the waterlily and the gerber daisy. In these flowers the purpose of such an arrangement is to attract insects to their centres. The Sea Anemone is a radial animal, and so is a Starfish, its five arms allow it to move in any direction.

When children make a paper flower or snowflake by folding a circle into eighths or sixths from the centre point and then cutting patterns into the folded sides and edge (circumference), they are part of a long tradition. Almost 500 years ago, Kepler wrote a book called the 6 Cornered Snowflake. He concluded upon examining the structure and pattern of snowflakes that matter is composed of identical units or atoms.

Logo programs can be written to simulate Von Koch's snowflake. The edges are equilateral triangles. The pattern is one of ever decreasing size as each new generation is added. The straight lines take on an illusion of curves, in the same way as curved stitching does. Information and pictures are easily attainable on the Internet.

Very young learners can use gummed paper triangles of different sizes to build a snowflake. By examining the pattern of growth they are able to estimate the number of triangles each generation needs.

Similar Logo programs can be written to show other branching patterns wherein sections get progressively smaller. The same type of branching that is seen in deer antlers, fern leaves, blood vessels and TV aerials as well as trees. The results of these programmes amaze young learners and give them early exposure to the concept of fractals!

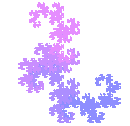
All of these patterns and we have hardly mentioned the simplest of all pattern, numeric. Even the natural world is loaded with numeric pattern: from the regular 28 days lunar cycle, the annual cycle of 365 and a quarter days to the number of legs on animals. Legs? Yes, humans have 2, cows have 4, bees have 6, spiders have 8. Why even flowers' petals are not exempt from the power of pattern. Lilies have 3, buttercups have 5, delphiniums have 8, marigolds have 13, asters 21 and daisies 34. It took 800 years to explain why this series of numbers that Leonardo of Pisa (Fibonacci) identified is rampant in nature, just like the rabbits in the problem he devised. We haven't even got to the golden ratio, Pascal's or Omar Khayam's triangles, multiples and ...

As Ian Stewart noted, all pattern can be expressed by number. We can recreate nature's shapes by finding and plotting co-ordinates. Did we mention co-ordinates? No, the problem is not lack of material to choose from in studying pattern, the problem is lack of time.