A Mixed-up Clock printable sheet

Here is a clock face where the numbers have become all mixed up. In the picture, each of the numbers is represented by a letter. Can you find out which letter represents which number using the ten statements below?

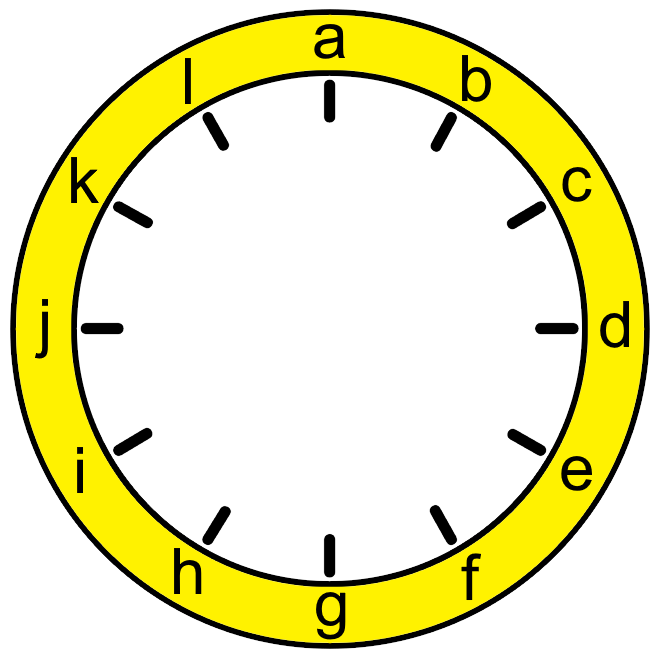
1. No even number is between two odd numbers.
2. No consecutive numbers are next to each other.
3. The numbers on the vertical axis (a and g) add to $13$.
4. The numbers on the horizontal axis (d and j) also add to $13$.
5. The first set of $6$ numbers (a, b, c, d, e, f) add to the same total as the second set of $6$ numbers (g, h, i, j, k, l).
6. The number at position f is in the correct position on the clock face.
7. The number at position d is double the number at position h.
8. There is a difference of $6$ between the number at position g and the number before it (f).
9. The number at position l is twice the top number (a), one third of the number at position d and half of the number at position e.
10. The number at position d is $4$ times one of the numbers next to it.