Copyright © University of Cambridge. All rights reserved.
'Polite Numbers' printed from https://nrich.maths.org/
Show menu
Christopher and Atharv from Trevelyan Middle School and Scout from the UK found that 63 is polite. Atharv wrote:
63 is a polite number because 31+32= 63
Miraya from Heckmondwike Grammar School in the UK set up an equation:
(THE CONSECUTIVE NUMBERS)
$x+x+1=63$
$2x+1=63$
$2x=63-1$
$2x=62$
$x=62\div2$
$x=31$
David from IES Maximo Laguna in Spain found lots of other ways:
it can be the result of different sums:
6+7+8+9+10+11+12=63
20+21+22=63
3+4+5+6+7+8+9+10+11=63
31+32=63
Adding three consecutive integers, Miraya noticed:
If you add up three consecutive integers ,you get multiples of 3.
E.g. 1+2+3=6 2+3+4=9 3+4+5=12 4+5+6=15 5+6+7=18 6+7+8=21 7+8+9=24 8+9+10=27 9+10+11=30 10+11+12=33 11+12+13=36 12+13+14=39 13+14+15=42
14+15+16=45 ..ect.
ALL ARE MULTIPLES OF THREE!
Mahdi from Mahatma Gandhi International School in India represented the numbers algebraically:
In fact, Mahdi has shown that all sums of 3 consecutive integers are multiples of 3, but there could be a multiple of 3 which is not polite! However, this algebra is sufficient, since $n+1$ could be any number, so $3(n+1)$ could represent any multiple of 3.
Jiali from LAE Tottenham in the UK tried adding different numbers of consecutive numbers:
Miraya and David also came to the conclusion that multiples of 5 are all polite. Mahdi used algebra again:
... since $n+2$ can be any integer, except $1$, all $5(n+2)$ can be any multiple of $5$ except $5$. But 5=2+3 so 5 is polite.
Christopher and Atharv found an impolite number:
One is an impolite number.
Agrim from ABQ Education Group in Oman and Jiali identified all the impolite numbers up to 20. Here is Agrim's work:
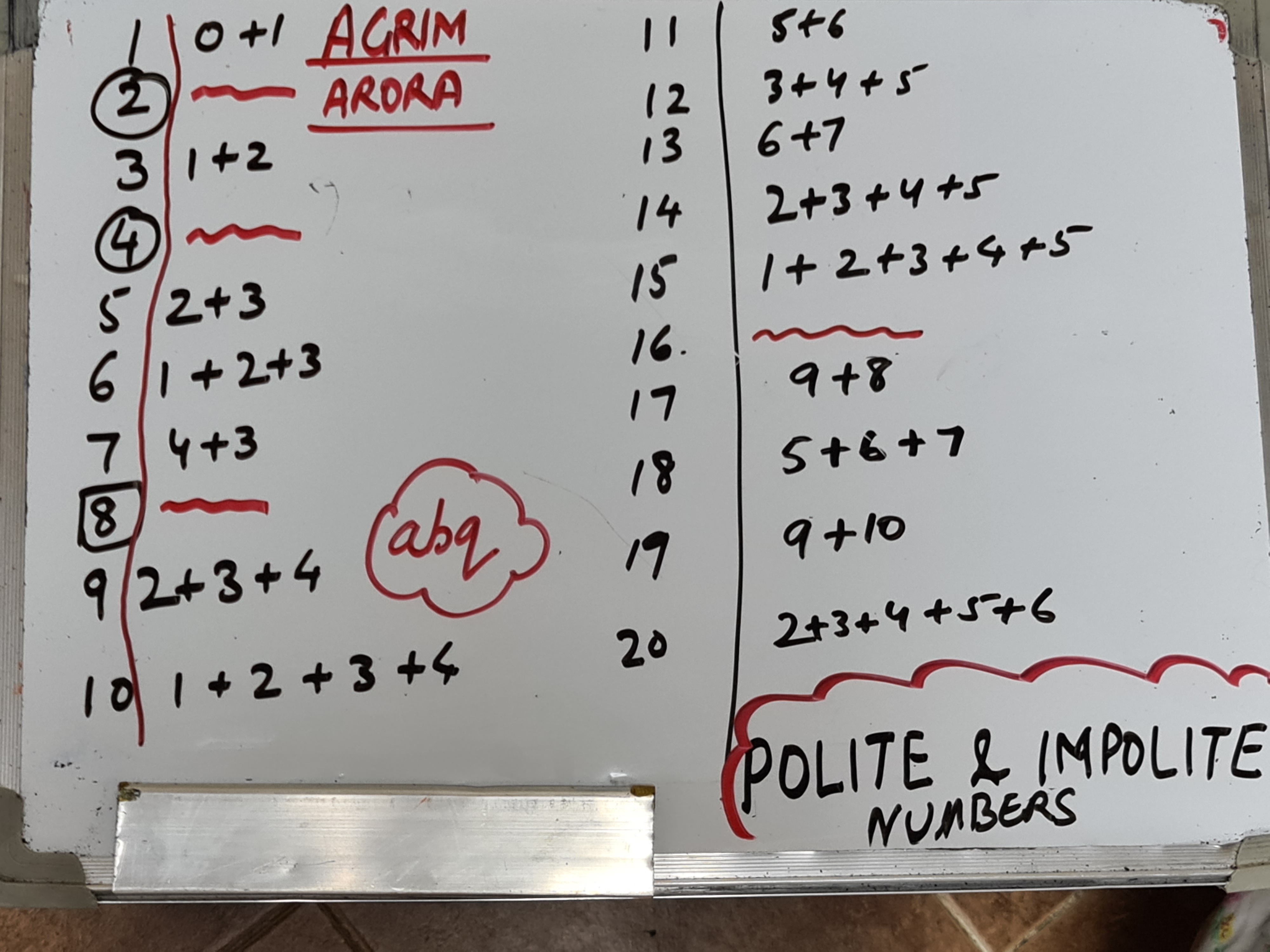
David wrote that 1 is the only odd impolite number. Jiali showed why:
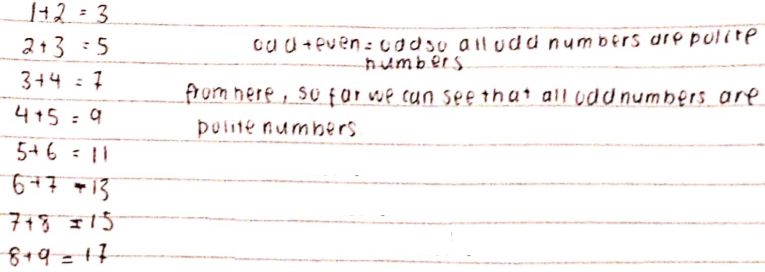
Just like in Mahdi's proof, it is important to notice that not only are all the sums odd, but that all odd numbers can be written in this way (since they go 3, 5, 7, 9... it does look like they can)
Scout and David noticed something about them. Scout wrote:
64 must be impolite since consecutive integers cannot be formed with 2 or 3 consecutive numbers. While 64$\div$4=16, 14, 15, 16 and 17 do not add to 64. I though this may apply to all powers of two- so I tested the first three of them below:
2- the only numbers here could be 0,1. Two ones would form two, but these are the same number so not consecutive.
4- 1,2,3 are the available numbers. 1+2+3=6. 1+2=3. 2+3=5. These are the only available consecutive numbers for this set.
8- 1,2,3,4,5,6,7, are the available numbers here. 1+2=3. 2+3=5. 3+4=5, 4+5=9. ( It is evident here that the further numbers will be in excess of 8).
We can see that after 2 (which must be impolite since it only has one number smaller than it) the powers of two are halfway through (in for number eight 3.5 and 4.5 would add to 8 but these are not integers). I have algebraically proven this in my image.
Unfortunately, we cannot access Scout's proof. David wrote the rule that Scout described, and some explanations:
Powers of 2 are impolite; other positive integers can be expressed as the sum of [consecutive] positive integers.
The rule works for several reasons:
1- Firstly, the number of numbers you add to make a polite number is the same as the difference [between the polite number and] the next polite number you can make adding the same number of numbers minus. For example: 1+2+3+4=10. 4 numbers are added. The next sequence of numbers that you can form with this number of numbers is 2+3+4+5=14. 14-10=4.
2- In addition, to get the sum that results in a polite number, you have to divide that number by one of its odd factors. That factor indicates the number of numbers that make up the sum. The result of the division is the number that is in the centre of the sum. For example: 21$\div$3=7.
3 is a factor of 21 and is the number of numbers that are in the sum. 7 is the central number of the sum, so the result is 6+7+8=21.
3- The factor you divide the polite number by must meet the following rule in order to express the sum.
$\frac{N-1}2 \leq M$ $N$: factor $M$: result of the division.
If this rule is not met, that factor cannot divide the polite number to obtain the sum. This is the case of using 11 to divide 33, where negative numbers would be needed to complete the sum.
4- Prime numbers other than 2 are divided by 2 to get their sum. For example: 11$\div$2= 5.5. Since 5.5 is between 5 and 6 and you need 2 positive integers, the sum is expressed as 5+6.
5- Powers of 2 do not meet the above rules and would need negative numbers to express the sum that make them up, therefore, they are impolite numbers.
6- Finally, taking into account that the previous rules are fulfilled, we can get different sums for a polite number, either dividing it between odd factor or between even numbers until getting a prime number and use the fourth rule.
Jiali used David's ideas 2, 3 and 4 to prove that all powers of 2 are impolite:
Mahdi and another David, from the UK, all proved that all powers of 2 are impolite using a formula. This is Mahdi's work, which begins with two proofs of the formula:
(by parity, we mean "even or odd-ness", so if two numbers have opposite parity, then one is even and the other is odd)
Sanika from PBBMS, OMR in India also proved that no power of 2 is a polite number:
Sum of an arithmetic sequence can be found from the formula $\text{Sum}=\dfrac{n(a+b)}{2}$
Here, $n$ stands for the number of elements in the sequence. $a$ is the first element of the sequence and $b$ is the last element of the sequence.
In this case the sequence consists of consecutive numbers, so the number of elements will be $b-a+1.$ So, the sum is $\dfrac{\left(a+b\right)(\ b-a+1)}{2}$
Say we want to check if the number $t$ is polite, then we should be able to represent $2t$ as the product of $\left(a+b\right)(\ b-a+1).$
But $(a+b)-(b-a+1)=2a-1$
Since the smallest value that $a$ can take up is $1$, we can say that $2a-1$ represents all the odd numbers.
Therefore if $2t$ can be represented as a product of $2$ numbers with an odd difference, then $t$ is a polite number.
Actually, this should be the other way round: If $t$ is a polite number (Sanika's initial assumption), then $2t$ can be represented as a product of $2$ numbers with an odd difference (what Sanika has shown from the initial assumption).
Prime factoring $2t$ can give us 3 different cases:
Case1: the prime factors consist of odd numbers and one $2.$ For example if $t=35,$ then the prime factors of $2t$ are $2\times5\times7$
Case2: the prime factors consist of even numbers. E.g. If $t=16$ then $2t= 2\times2\times2\times2\times2$
Case3: the prime factors consist of a mixture of even and odd numbers. E.g. If $t=30$ then $2t=2\times2\times3\times5$
In the first case you can take one of the factors of $2t$ as $2$ and the other factor as the product of the rest of the odd numbers (which will be odd). The difference of these two factors will be odd.
There are no two even numbers that give an odd difference. And as the product of $2$ even numbers will always be even, you cannot find two 2 factors following the criteria in case 2.
However, in case 3 you can make the first factor the product of all the odd numbers in the prime factorisation and the second factor the product of all even numbers. The difference of these 2 factors will be odd.
Therefore, all numbers with a totally even factorisation i.e., powers of 2, will make up the group of impolite numbers. All other numbers will be polite.
Sanika and Mahdi have proved that all powers of 2 are impolite, because their proofs began with a polite number called $t$ or $s$ and showed that $t$ or $s$ couldn't be a power of 2. However, the final assertion that all other numbers are polite was only proved successfully by David from the UK:
This expression is derived in Mahdi's and Sanika's proofs. David will show that for any number $n$, there is an $m$ and an $r$ so that $\frac12(m+1)(2r+m)=n$ unless $n$ is a power of 2.