Skip Counting

'Skip Counting' printed from https://nrich.maths.org/

Show menu

Skip Counting

Find the squares that Froggie skips onto to get to the pumpkin patch.

She starts on $3$ and finishes on $30$, but she lands only on a square that has a number $3$ more than the square she skips from.

A numbered grid for Froggie to fidn her way to the pumpkin patch.

Is there more than one way that Froggie can get to the pumpkins?

Why do this problem?

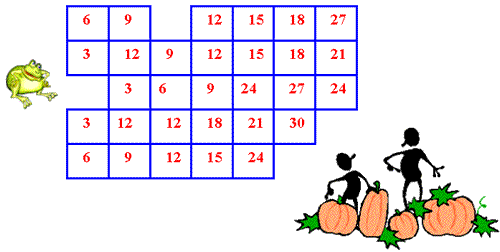
This problem provides an appealing context for practising the three times table. It gives an opportunity for children to realise that there is not necessarily just one answer to a mathematical problem.

Children might find it helpful to use this sheet of the grid with counters.

Key questions

How are you deciding where to go?

Which square could we go to next?
Do you think there are more than one route?
If so, how you you find it?
Is there a way of remembering your route?

Possible extension

Invent a similar activity that would mean Froggie only jumped on a square that is four more than where she is. So you choose which numbers go where.

Possible support

You could suggest that children write out the numbers in the three times table first. They might also find it easier to start at $30$ and work backwards.