 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Marvellous Matrix



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Marvellous Matrix
This problem was written for new year $2002$.
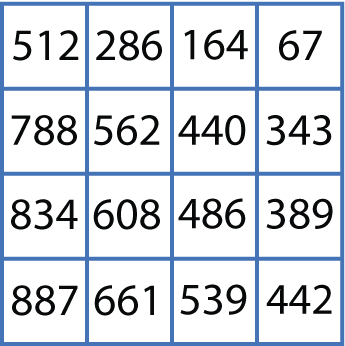
Circle any number in the matrix, for example, $608$ as below. Draw a line through all the squares that lie in the same row and column as your selected number.
Circle another number which has not got a line through it, for example, $343$ and again rule out all squares in the same row and column.
Repeat for a third time, then circle the remaining number which has not got a line through it.
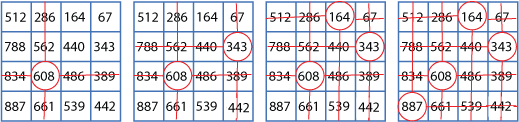
Add all the circled numbers together. Note your answer.
Try again with a different starting number. What do you notice?
See if you can work out how this matrix works.
Below is a simpler one which might be easier to investigate.
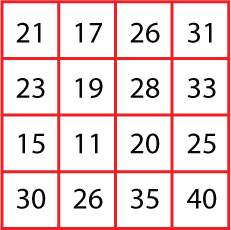
Can you make a similar matrix which generates a different total?
Why do this problem?
This problem is tricky to do but can form an interesting challenge to those who need it. It requires much addition & subtraction as well as the making and testing hypotheses.Key questions
Possible extension
Learners could make their own puzzle matrices.Possible support
Suggest doing a easier problem such as Shapes on the playground.You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.