 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Always Perfect



Always Perfect printable sheet - part 1
Always Perfect printable sheet - part 2
In this problem you will get the chance to discover some surprising results. Can you prove that they are always true?
Part 1(a)
Take two numbers that differ by 2, multiply them together and add 1 (so for example $5 \times 7 + 1 = 36$).
Try this for some more pairs of numbers which differ by 2.
What do you notice? Is this always true? Can you prove your conjecture?
After you've had a go at this problem you might like to take a look at what Claire and Charlie did:
Charlie drew an n by n+2 rectangle, then split it up and rearranged it to almost make a square...
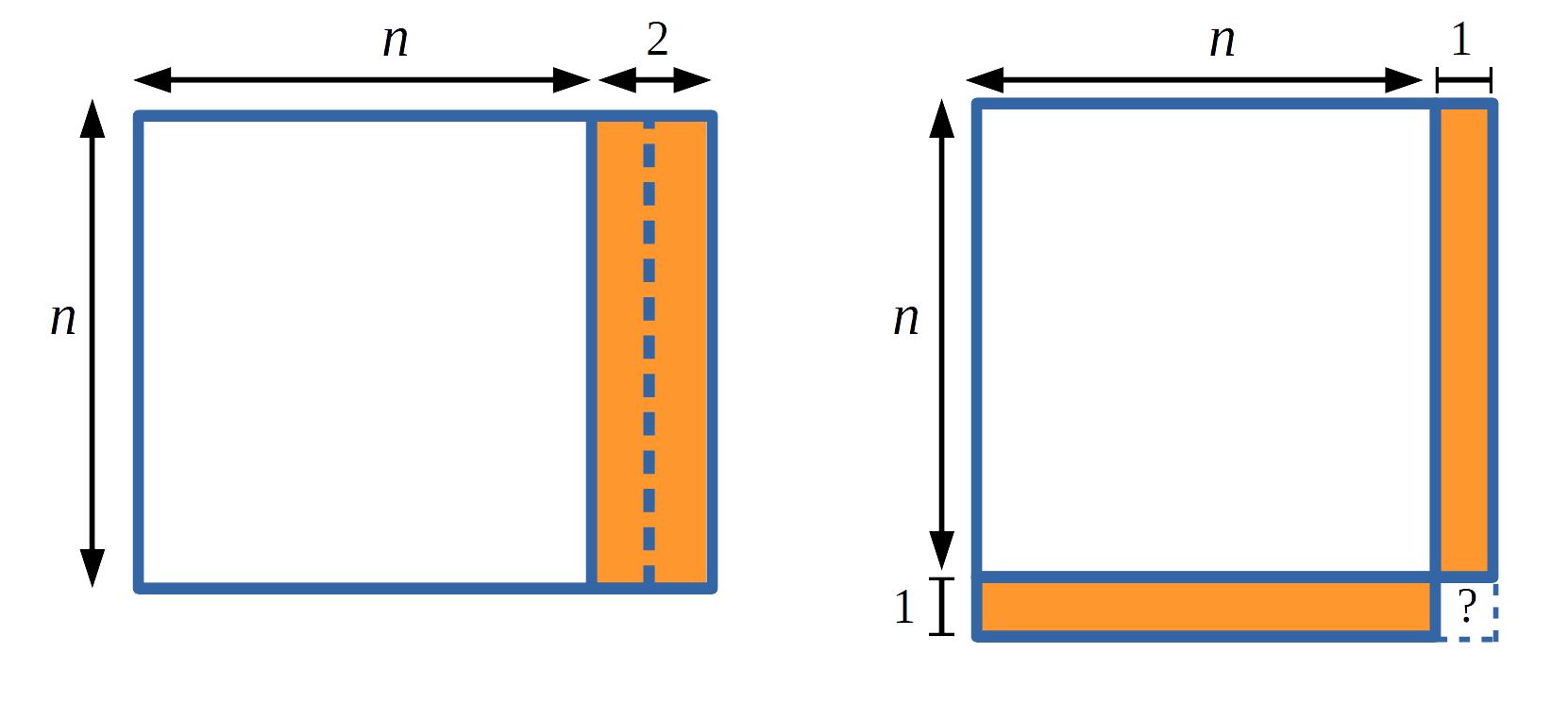
Claire expressed what she discovered algebraically: $$n(n+2) + 1 = n^2 + 2n + 1\\ \hspace{20mm} = (n + 1)^2$$
Part 1(b)
Now take two numbers that differ by 4, multiply them together and add 4
(so for example $5 \times 9 + 4 = 49$).
Try this for some more pairs of numbers which differ by 4.
What do you notice? Is this always true? Can you prove your conjecture?
Part 1(c)
Now take two numbers that differ by 6, multiply them together and add 9.
Try this for some more pairs of numbers which differ by 6.
What do you notice? Is this always true? Can you prove your conjecture?
Part 1(d)
Looking at your results for parts (a), (b) and (c) can you predict what you will have to add to the product of two numbers that differ by $8, 10, 12, ..., 2k$ in order to get a square number?
Can you write down a general statement? Can you prove this statement?
---------------
Part 2(a)
Now consider what happens when $1$ is added to the product of four consecutive numbers, for example $2\times 3 \times 4 \times 5 + 1 = 121$.
Try this for some other sets of four consecutive numbers.
What do you notice? Is this always true? Can you prove your conjecture?
After you've had a go at this problem you might like to take a look at what Claire and Charlie did:
Charlie noticed a relationship between the product of the first and last of the four consecutive numbers, and the solution:
$$2\times 3 \times 4 \times 5 + 1 = 121 = (10 + 1)^2$$ $$3\times 4 \times 5 \times 6+ 1 = 361 = (18 + 1)^2$$ He then used this to help him write the general rule algebraically and check that it worked
Claire expressed what she was doing algebraically: $$n(n+1)(n+2)(n+3) + 1 = n^4+ 6n^3 + 11n^2 + 6n + 1$$ and then she tried to factorise this to find a squared expression
Part 2(b)
Now take four consecutive even numbers (or four consecutive odd numbers), multiply them together and add 16 (so for example $2\times 4 \times 6 \times 8 + 16 = 400$).
Try this for some more sets of four consecutive even (or odd) numbers.
What do you notice? Is this always true? Can you prove your conjecture?
Part 2(c)
Now take four numbers which differ by 3, multiply them together and add 81
(so for example $2\times 5 \times 8 \times 11 + 81 = 961$).
Try this for some more sets of four numbers which differ by 3.
What do you notice? Is this always true? Can you prove your conjecture?
Part 2(d)
Looking at your results for parts (a), (b) and (c) can you predict what you will have to add to the product of four numbers that differ by $4, 5, 6, ..., k$ in order to get a square number?
Can you write down a general statement? Can you prove this statement?
Although number theory - the study of the natural numbers - does not typically feature in school curricula it plays a leading role in university at first year and beyond. Having a good grasp of the fundamentals of number theory is useful across all disciplines of mathematics. Moreover, problems in number theory are a great leisure pastime as many require only minimal knowledge of mathematical 'content'.
We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.