Cherri, Saxon, Mel and Paul are friends. They are all different ages: $5, 6, 7$ and $8$ years old.

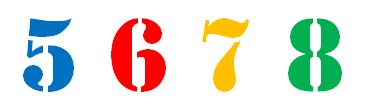
Can you find out the age of each friend?


Use these clues to help you:
 

Saxon's age is an even number.

Mel and Paul's ages added together are double Saxon's age.

Mel's age is half of Cherri and Saxon's ages added together.

Mel and Paul's ages are both odd numbers.