You may also like

problem icon

I'm Eight

Find a great variety of ways of asking questions which make 8.

problem icon

Calendar Capers

Choose any three by three square of dates on a calendar page. Circle any number on the top row, put a line through the other numbers that are in the same row and column as your circled number. Repeat this for a number of your choice from the second row. You should now have just one number left on the bottom row, circle it. Find the total for the three numbers circled. Compare this total with the number in the centre of the square. What do you find? Can you explain why this happens?

problem icon

GOT IT Now

For this challenge, you'll need to play Got It! Can you explain the strategy for winning this game with any target?

Jugs of Wine

Stage: 3 Challenge Level: Challenge Level:2 Challenge Level:2

This is a very well-explained solution submitted by Julia (Wymondham High School):


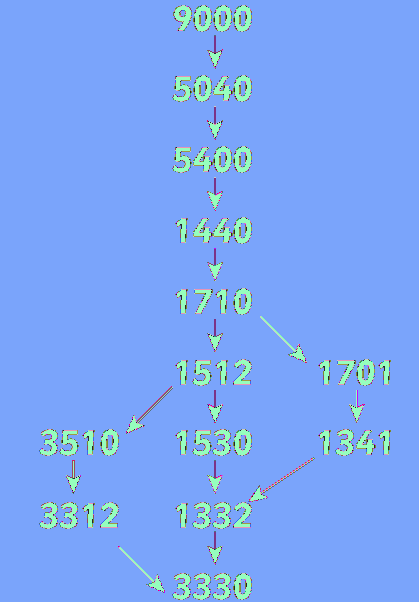
For the jugs holding 9, 7, 4, and 2 litres, this flow diagram shows how the solution can be achieved in three distinct ways, using eight decantings of the wine. In each case, the 9 litres of wine are being poured back and forth to achieve the required result. We order the jugs by size and use a four digit number to represent the volume of wine in each jug. For example 9000 means there are 9 litres in the 9 litre jug, and the 7, 4 and 2 litre jugs are empty. The solution is found when we have 3330, where 3 litres are in each of the 9, 7 and 4 litre jugs; and the 2 litre jug is empty.


To measure out all the integer amounts from 1 to 8 litres using three jugs, one of which is full and holds 8 litres, there are several possible solutions. For example, for jugs with capacities 8, 3 and 2 litres, the following triples give the numbers of litres in each of the jugs at successive steps and all the amounts from 1 litre to 8 litres occur at some stage of the process: (8,0,0) (5,3,0) (5,1,2) (7,1,0) (7,0,1) (6,0,2) (6,2,0) (4,2,2). There are other solutions for capacities of 8, 4 and 3; for 8, 5 and 4; for 8, 5 and 1 etc.

 

Two other different students from Wymondham High School, David and Rachel, also submitted good solutions. In their answers, they included a very useful table of results which showed at a glance the state of the jugs after any particular pouring.


Much later two students from Flegg High, Luke and Ian, also submitted a successful solution to this problem. They had found their answer after "hours of trouble, and help from Mrs Fenn".



The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.