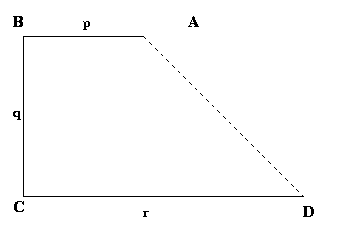
Three rods of lengths $p$, $q$ and $r$ with $p< q< r$ are arranged to form three sides $AB$, $BC$ and $CD$ of an enclosure $ABCD$ with right angles at $B$ and $C$. The diagram shows one possibility but the rods can be exchanged to make different enclosures. The enclosure is completed by joining $A$ and $D$. How should the rods be arranged to make the area of the enclosure as big as possible?