Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Xtra
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Two solutions to this problem have been forthcoming from different students at the same school - Madras College. Thank you to Mike and Euan who used lots of trigonometry as well as to Thom who likewise resorted to double angles and the cosine rule and reduced the problem to solving a quadratic equation. Thom was also able to show the significance of the two roots.
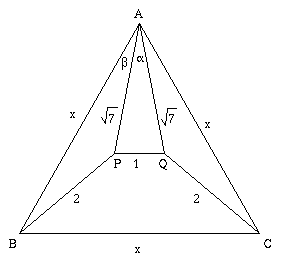
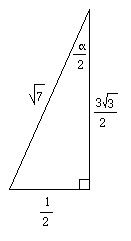
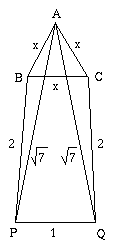
A solution which just needs Pythagoras's Theorem was sent in by Ewan from King Edward VII School, Sheffield. See if you can work it out from the diagram below, then reveal the hidden text to check your answer.

The diagram shows the median AU at point A cutting the triangle in half. The length AU is in two parts, $y$ and $z$. Since the triangle is equilateral, $y+z=\frac{\sqrt 3}{2}x$. (You may like to prove this e.g. by trigonometry) To work out $y$ use Pythagoras's Theorem:
\begin{align}
y^2+\left(\frac{1}{2}\right)^2 &=\left(\sqrt 7\right)^2 \\
y^2 &= \frac{27}{4} \\
y &= \frac{3\sqrt 3}{2}
\end{align}
and use $y+z=\frac{\sqrt 3}{2}x$ to give $z = (x-3)\frac{\sqrt 3}{2}$.
Then more Pythagoras's Theorem and our values found above give
\begin{align}
z^2+\left(\frac{x}{2} - \frac{1}{2}\right)^2 &=2^2 \\
\frac{3(x-3)^2}{4} + \frac{(x-1)^2}{4} = 4
\end{align}
which simplifies to get the same equation as Thom and the others: $x^2 -5x + 3 = 0$.
What a simple solution, Well done!
\begin{align}
y^2+\left(\frac{1}{2}\right)^2 &=\left(\sqrt 7\right)^2 \\
y^2 &= \frac{27}{4} \\
y &= \frac{3\sqrt 3}{2}
\end{align}
and use $y+z=\frac{\sqrt 3}{2}x$ to give $z = (x-3)\frac{\sqrt 3}{2}$.
Then more Pythagoras's Theorem and our values found above give
\begin{align}
z^2+\left(\frac{x}{2} - \frac{1}{2}\right)^2 &=2^2 \\
\frac{3(x-3)^2}{4} + \frac{(x-1)^2}{4} = 4
\end{align}
which simplifies to get the same equation as Thom and the others: $x^2 -5x + 3 = 0$.
What a simple solution, Well done!