Pericut

Two semicircle sit on the diameter of a semicircle centre O of twice their radius. Lines through O divide the perimeter into two parts. What can you say about the lengths of these two parts?

Five Circuits, Seven Spins

A circular plate rolls inside a rectangular tray making five circuits and rotating about its centre seven times. Find the dimensions of the tray.

Squareflake

A finite area inside and infinite skin! You can paint the interior of this fractal with a small tin of paint but you could never get enough paint to paint the edge.

Belt

Stage: 5 Challenge Level:

Herbert of Sha Tin College, Hong Kong submitted the only correct solution to date which is given below. Can anyone give an alternative solution?

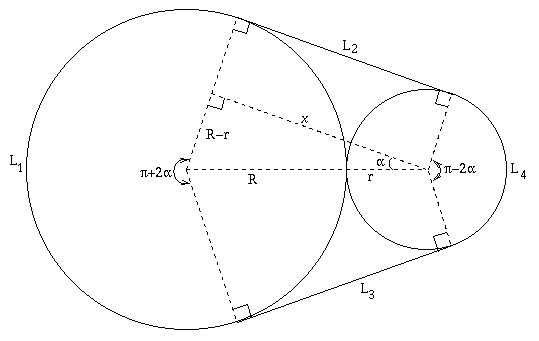$\alpha = \sin^{-1}(R - r)/(R + r)$

$L_1 = R(\pi + 2\alpha)$

$L_4 = r(\pi - 2\alpha)$

$L_2 = L_3 = x$

$x^2 = (R + r)^2 - (R - r)^2$

$x^2 = 4Rr$

$x = 2\sqrt{Rr}$

$L_2 + L_3 = 4\sqrt{Rr}$

The total length $L$ is $4\sqrt{Rr} + \pi(R + r) + 2(R -r)\sin^{-1}(R - r)/(R + r).$

Perimeters. Circles. Pythagoras' theorem. Arcs, sectors and segments. Cartesian equations of circles. Cosine. Tangents. Complex numbers. Tangent. Sine.

You may also like

Pericut

Five Circuits, Seven Spins

Squareflake

Belt

Stage: 5 Challenge Level: