Squ-areas

Sue, Madras College, arrived at the correct answer using the formula $\frac{1}{2}ab \sin C$. For those not familiar with this formula then do look again at the problem. You may find a more accessible solution if you remember Pythagoras and that:

$26 = 5^2 + 1^2$
$20 = 4^2 + 2^2$
$18 = 3^2 + 3^2$.

This solution was submitted by Sue.

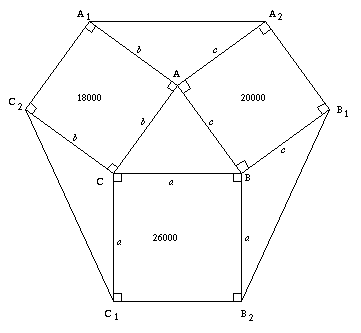
First we change square centimeters into square metres, so $26000$ cm$^2 = 2.6$ m$^2$ , $18000$ cm $^2 = 1.8$ m$^2$ and $20000$ cm$^2 = 2$ m$^2$.

Then we put letters at all points shown on the diagram so the three enclosed triangles are triangle $CC_1C_2$, triangle $BB_1B_2$, and triangle $AA_1A_2$.

Let the length of $AB$ be $c$, length of $AC$ be $b$ and the length of $BC$ be $a$. Because of the squares, $BB_1 = AA_2 = c$, $AA_1 = CC_2 = b$ and $CC_1 = BB_2 = a$.

We know the formula for the area of a triangle $ABC$ is $(1/2)absin C$.

In triangle $CC_1C_2$

$CC_1 = CB = a$

$CC_2 = AC = b$

$\sin(180^{\circ} - C) = \sin C$ (because of the two right angles)

so triangle $CC_1C_2$ and triangle $ABC$ are equal in area.

Similarly we can prove triangle $AA_1A_2$ and triangle $BB_1B_2$ are also equal in area to triangle $ABC$. Therefore the four triangles are equal in area and we only need to work out one of these areas.

Using the formula $(1/2)ab \sin C$

Area of triangle $ABC$ = $1/2(\sqrt{2.6})(\sqrt{1.8})\sin{C}$ m$^2$

Using the cosine rule we can work out that

$\eqalign{ \cos{C} &=& \frac{2.6 + 1.8 - 2}{2\sqrt{2.6}\sqrt{1.8}} \\ \; &=& \frac{1.2}{\sqrt{4.68}} \\ \; &=& \frac{2}{\sqrt{13}}}$

Therefore we know that

$\eqalign{ \sin{C} &=& \frac{\sqrt{13 - 2^{2}}}{\sqrt{13}} \\ \; &=& \frac{3}{\sqrt{13}}}$

Put this in our original equation

$\eqalign{ \mbox{Area of triangle} ABC &=& 1/2(\sqrt{4.68})(\frac{3}{\sqrt{13}}) m^2 \\ \; &=& 1/2(0.6\sqrt{13})(\frac{3}{\sqrt{13}}) m^2 \\ \; &=& 0.9 m^2}$

Therefore the area of the hexagon is

(0.9 m$^2$ \times4) + 2.6 m$^2$ + 1.8 m$^2$+ 2 m$^2$	= 3.6 m$^2$ + 6.4 m$^2$
	= 10 m$^2$
	= 100000 cm$^2$