 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Two Triangles in a Square



- Problem
- Student Solutions
You may like to ponder the fact that, looking at David's diagram below, the square $LPKJ$ is 1/5th of the area of the square $ABCD$.
The following solution came from David (Madras College).
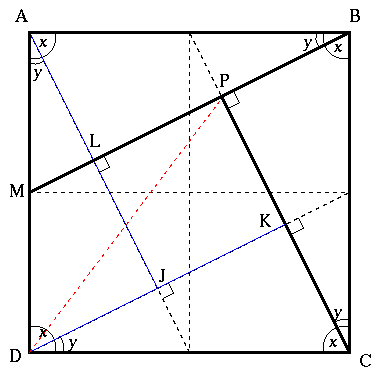
Label angles $x$ and $y$, where $x + y = 90^{\circ}$, $\angle MBC = x$ and $\angle ABM = y$
A line is drawn from point $A$ to point $L$ so that $\angle ALB = 90^{\circ}$
Triangles $ABL$ and $BCP$ are congruent because they have equal angles and $AB = BC$. Similarly triangles $CDK$ and $DAJ$ can be proven congruent with $ABL$ and $BCP$ forming a "camera shutter'' shape.
Triangle $ABM$ is similar to the four congruent triangles (with angles $x$, $y$ and $90^{\circ}$) and therefore the proportions are the same.
Because $AB = 2AM$ we have $PC = 2PB$ and then, as $KC = PB$, we have $PC = 2KC$, so $K$ is the midpoint of the line $PC$.
When triangle $CDK$ is reflected along the line $DK$, the line $DP$ is the reflection of the line $DC$ and they are therefore the same length.